bezier.hazmat.geometric_intersection module¶
Helpers for intersecting Bézier curves via geometric methods.
The functions here are pure Python and many have equivalent implementations written in Fortran and exposed via a Cython wrapper.
- bezier.hazmat.geometric_intersection.bbox_intersect(nodes1, nodes2)¶
Bounding box intersection predicate.
Note
There is also a Fortran implementation of this function, which will be used if it can be built.
Determines if the bounding box of two sets of control points intersects in \(\mathbf{R}^2\) with non-trivial intersection (i.e. tangent bounding boxes are insufficient).
Note
Though we assume (and the code relies on this fact) that the nodes are two-dimensional, we don’t check it.
- Parameters:
nodes1 (numpy.ndarray) – Set of control points for a Bézier shape.
nodes2 (numpy.ndarray) – Set of control points for a Bézier shape.
- Returns:
Enum from
BoxIntersectionTypeindicating the type of bounding box intersection.- Return type:
- bezier.hazmat.geometric_intersection.linearization_error(nodes)¶
Compute the maximum error of a linear approximation.
Note
There is also a Fortran implementation of this function, which will be used if it can be built.
Note
This is a helper for
Linearization, which is used during the curve-curve intersection process.We use the line
\[L(s) = v_0 (1 - s) + v_n s\]and compute a bound on the maximum error
\[\max_{s \in \left[0, 1\right]} \|B(s) - L(s)\|_2.\]Rather than computing the actual maximum (a tight bound), we use an upper bound via the remainder from Lagrange interpolation in each component. This leaves us with \(\frac{s(s - 1)}{2!}\) times the second derivative in each component.
The second derivative curve is degree \(d = n - 2\) and is given by
\[B''(s) = n(n - 1) \sum_{j = 0}^{d} \binom{d}{j} s^j (1 - s)^{d - j} \cdot \Delta^2 v_j\]Due to this form (and the convex combination property of Bézier Curves) we know each component of the second derivative will be bounded by the maximum of that component among the \(\Delta^2 v_j\).
For example, the curve
\[\begin{split}B(s) = \left[\begin{array}{c} 0 \\ 0 \end{array}\right] (1 - s)^2 + \left[\begin{array}{c} 3 \\ 1 \end{array}\right] 2s(1 - s) + \left[\begin{array}{c} 9 \\ -2 \end{array}\right] s^2\end{split}\]has \(B''(s) \equiv \left[\begin{array}{c} 6 \\ -8 \end{array}\right]\) which has norm \(10\) everywhere, hence the maximum error is
\[\left.\frac{s(1 - s)}{2!} \cdot 10\right|_{s = \frac{1}{2}} = \frac{5}{4}.\]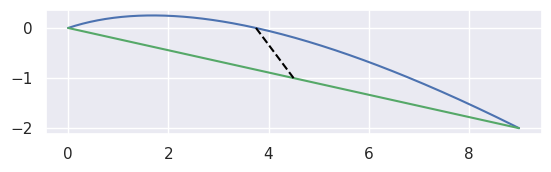
>>> import numpy as np >>> nodes = np.asfortranarray([ ... [0.0, 3.0, 9.0], ... [0.0, 1.0, -2.0], ... ]) >>> linearization_error(nodes) 1.25
As a non-example, consider a “pathological” set of control points:
\[\begin{split}B(s) = \left[\begin{array}{c} 0 \\ 0 \end{array}\right] (1 - s)^3 + \left[\begin{array}{c} 5 \\ 12 \end{array}\right] 3s(1 - s)^2 + \left[\begin{array}{c} 10 \\ 24 \end{array}\right] 3s^2(1 - s) + \left[\begin{array}{c} 30 \\ 72 \end{array}\right] s^3\end{split}\]By construction, this lies on the line \(y = \frac{12x}{5}\), but the parametrization is cubic: \(12 \cdot x(s) = 5 \cdot y(s) = 180s(s^2 + 1)\). Hence, the fact that the curve is a line is not accounted for and we take the worse case among the nodes in:
\[\begin{split}B''(s) = 3 \cdot 2 \cdot \left( \left[\begin{array}{c} 0 \\ 0 \end{array}\right] (1 - s) + \left[\begin{array}{c} 15 \\ 36 \end{array}\right] s\right)\end{split}\]which gives a nonzero maximum error:
>>> nodes = np.asfortranarray([ ... [0.0, 5.0, 10.0, 30.0], ... [0.0, 12.0, 24.0, 72.0], ... ]) >>> linearization_error(nodes) 29.25
Though it may seem that
0is a more appropriate answer, consider the goal of this function. We seek to linearize curves and then intersect the linear approximations. Then the \(s\)-values from the line-line intersection is lifted back to the curves. Thus the error \(\|B(s) - L(s)\|_2\) is more relevant than the underlying algebraic curve containing \(B(s)\).Note
It may be more appropriate to use a relative linearization error rather than the absolute error provided here. It’s unclear if the domain \(\left[0, 1\right]\) means the error is already adequately scaled or if the error should be scaled by the arc length of the curve or the (easier-to-compute) length of the line.
- Parameters:
nodes (numpy.ndarray) – Nodes of a curve.
- Returns:
The maximum error between the curve and the linear approximation.
- Return type:
- bezier.hazmat.geometric_intersection.segment_intersection(start0, end0, start1, end1)¶
Determine the intersection of two line segments.
Assumes each line is parametric
\[\begin{split}\begin{alignat*}{2} L_0(s) &= S_0 (1 - s) + E_0 s &&= S_0 + s \Delta_0 \\ L_1(t) &= S_1 (1 - t) + E_1 t &&= S_1 + t \Delta_1. \end{alignat*}\end{split}\]To solve \(S_0 + s \Delta_0 = S_1 + t \Delta_1\), we use the cross product:
\[\left(S_0 + s \Delta_0\right) \times \Delta_1 = \left(S_1 + t \Delta_1\right) \times \Delta_1 \Longrightarrow s \left(\Delta_0 \times \Delta_1\right) = \left(S_1 - S_0\right) \times \Delta_1.\]Similarly
\[\Delta_0 \times \left(S_0 + s \Delta_0\right) = \Delta_0 \times \left(S_1 + t \Delta_1\right) \Longrightarrow \left(S_1 - S_0\right) \times \Delta_0 = \Delta_0 \times \left(S_0 - S_1\right) = t \left(\Delta_0 \times \Delta_1\right).\]Note
Since our points are in \(\mathbf{R}^2\), the “traditional” cross product in \(\mathbf{R}^3\) will always point in the \(z\) direction, so in the above we mean the \(z\) component of the cross product, rather than the entire vector.
For example, the diagonal lines
\[\begin{split}\begin{align*} L_0(s) &= \left[\begin{array}{c} 0 \\ 0 \end{array}\right] (1 - s) + \left[\begin{array}{c} 2 \\ 2 \end{array}\right] s \\ L_1(t) &= \left[\begin{array}{c} -1 \\ 2 \end{array}\right] (1 - t) + \left[\begin{array}{c} 1 \\ 0 \end{array}\right] t \end{align*}\end{split}\]intersect at \(L_0\left(\frac{1}{4}\right) = L_1\left(\frac{3}{4}\right) = \frac{1}{2} \left[\begin{array}{c} 1 \\ 1 \end{array}\right]\).
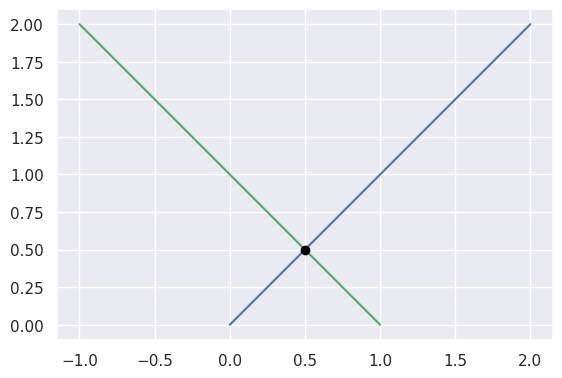
>>> start0 = np.asfortranarray([0.0, 0.0]) >>> end0 = np.asfortranarray([2.0, 2.0]) >>> start1 = np.asfortranarray([-1.0, 2.0]) >>> end1 = np.asfortranarray([1.0, 0.0]) >>> s, t, _ = segment_intersection(start0, end0, start1, end1) >>> s 0.25 >>> t 0.75
Taking the parallel (but different) lines
\[\begin{split}\begin{align*} L_0(s) &= \left[\begin{array}{c} 1 \\ 0 \end{array}\right] (1 - s) + \left[\begin{array}{c} 0 \\ 1 \end{array}\right] s \\ L_1(t) &= \left[\begin{array}{c} -1 \\ 3 \end{array}\right] (1 - t) + \left[\begin{array}{c} 3 \\ -1 \end{array}\right] t \end{align*}\end{split}\]we should be able to determine that the lines don’t intersect, but this function is not meant for that check:
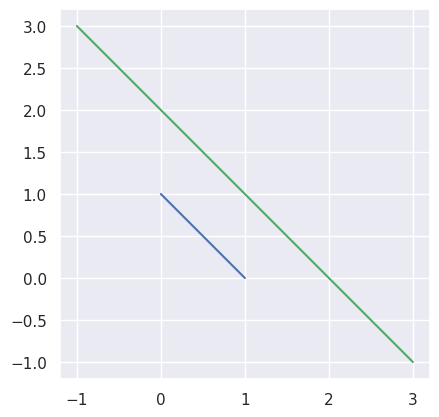
>>> start0 = np.asfortranarray([1.0, 0.0]) >>> end0 = np.asfortranarray([0.0, 1.0]) >>> start1 = np.asfortranarray([-1.0, 3.0]) >>> end1 = np.asfortranarray([3.0, -1.0]) >>> _, _, success = segment_intersection(start0, end0, start1, end1) >>> success False
Instead, we use
parallel_lines_parameters():>>> disjoint, _ = parallel_lines_parameters(start0, end0, start1, end1) >>> disjoint True
Note
There is also a Fortran implementation of this function, which will be used if it can be built.
- Parameters:
start0 (numpy.ndarray) – A 1D NumPy
2-array that is the start vector \(S_0\) of the parametric line \(L_0(s)\).end0 (numpy.ndarray) – A 1D NumPy
2-array that is the end vector \(E_0\) of the parametric line \(L_0(s)\).start1 (numpy.ndarray) – A 1D NumPy
2-array that is the start vector \(S_1\) of the parametric line \(L_1(s)\).end1 (numpy.ndarray) – A 1D NumPy
2-array that is the end vector \(E_1\) of the parametric line \(L_1(s)\).
- Returns:
Pair of \(s_{\ast}\) and \(t_{\ast}\) such that the lines intersect: \(L_0\left(s_{\ast}\right) = L_1\left(t_{\ast}\right)\) and then a boolean indicating if an intersection was found (i.e. if the lines aren’t parallel).
- Return type:
- bezier.hazmat.geometric_intersection.parallel_lines_parameters(start0, end0, start1, end1)¶
Checks if two parallel lines ever meet.
Meant as a back-up when
segment_intersection()fails.Note
This function assumes but never verifies that the lines are parallel.
In the case that the segments are parallel and lie on different lines, then there is a guarantee of no intersection. However, if they are on the exact same line, they may define a shared segment coincident to both lines.
In
segment_intersection(), we utilized the normal form of the lines (via the cross product):\[\begin{split}\begin{align*} L_0(s) \times \Delta_0 &\equiv S_0 \times \Delta_0 \\ L_1(t) \times \Delta_1 &\equiv S_1 \times \Delta_1 \end{align*}\end{split}\]So, we can detect if \(S_1\) is on the first line by checking if
\[S_0 \times \Delta_0 \stackrel{?}{=} S_1 \times \Delta_0.\]If it is not on the first line, then we are done, the segments don’t meet:
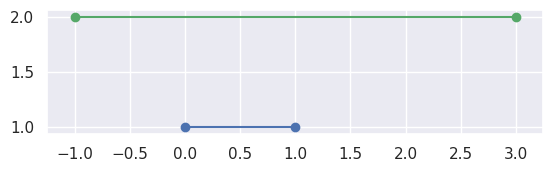
>>> # Line: y = 1 >>> start0 = np.asfortranarray([0.0, 1.0]) >>> end0 = np.asfortranarray([1.0, 1.0]) >>> # Vertical shift up: y = 2 >>> start1 = np.asfortranarray([-1.0, 2.0]) >>> end1 = np.asfortranarray([3.0, 2.0]) >>> disjoint, _ = parallel_lines_parameters(start0, end0, start1, end1) >>> disjoint True
If \(S_1\) is on the first line, we want to check that \(S_1\) and \(E_1\) define parameters outside of \(\left[0, 1\right]\). To compute these parameters:
\[L_1(t) = S_0 + s_{\ast} \Delta_0 \Longrightarrow s_{\ast} = \frac{\Delta_0^T \left( L_1(t) - S_0\right)}{\Delta_0^T \Delta_0}.\]For example, the intervals \(\left[0, 1\right]\) and \(\left[\frac{3}{2}, 2\right]\) (via \(S_1 = S_0 + \frac{3}{2} \Delta_0\) and \(E_1 = S_0 + 2 \Delta_0\)) correspond to segments that don’t meet:
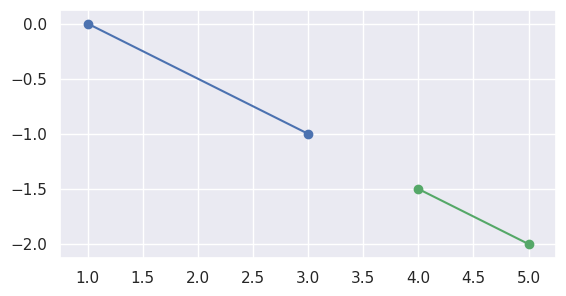
>>> start0 = np.asfortranarray([1.0, 0.0]) >>> delta0 = np.asfortranarray([2.0, -1.0]) >>> end0 = start0 + 1.0 * delta0 >>> start1 = start0 + 1.5 * delta0 >>> end1 = start0 + 2.0 * delta0 >>> disjoint, _ = parallel_lines_parameters(start0, end0, start1, end1) >>> disjoint True
but if the intervals overlap, like \(\left[0, 1\right]\) and \(\left[-1, \frac{1}{2}\right]\), the segments meet:
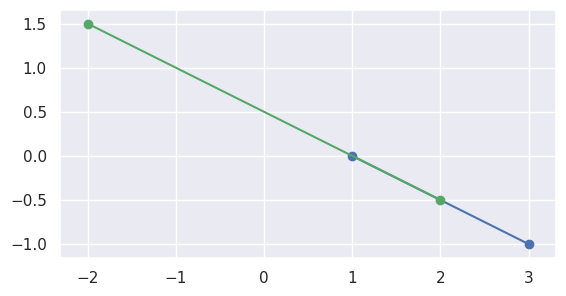
>>> start1 = start0 - 1.5 * delta0 >>> end1 = start0 + 0.5 * delta0 >>> disjoint, parameters = parallel_lines_parameters( ... start0, end0, start1, end1) >>> disjoint False >>> parameters array([[0. , 0.5 ], [0.75, 1. ]])
Similarly, if the second interval completely contains the first, the segments meet:
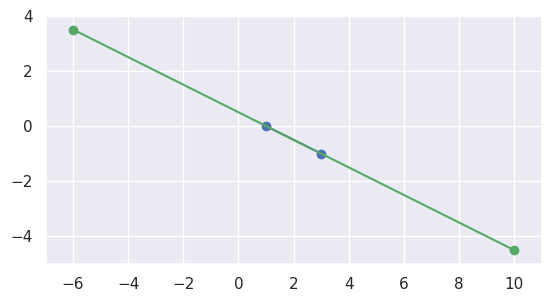
>>> start1 = start0 + 4.5 * delta0 >>> end1 = start0 - 3.5 * delta0 >>> disjoint, parameters = parallel_lines_parameters( ... start0, end0, start1, end1) >>> disjoint False >>> parameters array([[1. , 0. ], [0.4375, 0.5625]])
Note
This function doesn’t currently allow wiggle room around the desired value, i.e. the two values must be bitwise identical. However, the most “correct” version of this function likely should allow for some round off.
Note
There is also a Fortran implementation of this function, which will be used if it can be built.
- Parameters:
start0 (numpy.ndarray) – A 1D NumPy
2-array that is the start vector \(S_0\) of the parametric line \(L_0(s)\).end0 (numpy.ndarray) – A 1D NumPy
2-array that is the end vector \(E_0\) of the parametric line \(L_0(s)\).start1 (numpy.ndarray) – A 1D NumPy
2-array that is the start vector \(S_1\) of the parametric line \(L_1(s)\).end1 (numpy.ndarray) – A 1D NumPy
2-array that is the end vector \(E_1\) of the parametric line \(L_1(s)\).
- Returns:
A pair of
Flag indicating if the lines are disjoint.
An optional
2 x 2matrix ofs-tparameters only present if the lines aren’t disjoint. The first column will contain the parameters at the beginning of the shared segment and the second column will correspond to the end of the shared segment.
- Return type:
- bezier.hazmat.geometric_intersection.line_line_collide(line1, line2)¶
Determine if two line segments meet.
This is a helper for
convex_hull_collide()in the special case that the two convex hulls are actually just line segments. (Even in this case, this is only problematic if both segments are on a single line.)- Parameters:
line1 (numpy.ndarray) –
2 x 2array of start and end nodes.line2 (numpy.ndarray) –
2 x 2array of start and end nodes.
- Returns:
Indicating if the line segments collide.
- Return type:
- bezier.hazmat.geometric_intersection.convex_hull_collide(nodes1, nodes2)¶
Determine if the convex hulls of two curves collide.
Note
This is a helper for
from_linearized().- Parameters:
nodes1 (numpy.ndarray) – Control points of a first curve.
nodes2 (numpy.ndarray) – Control points of a second curve.
- Returns:
Indicating if the convex hulls collide.
- Return type:
- bezier.hazmat.geometric_intersection.from_linearized(first, second, intersections)¶
Determine curve-curve intersection from pair of linearizations.
Note
This assumes that at least one of
firstandsecondis not a line. The line-line case should be handled “early” bycheck_lines().Note
This assumes the caller has verified that the bounding boxes for
firstandsecondactually intersect.If there is an intersection along the segments, adds that intersection to
intersections. Otherwise, returns without doing anything.- Parameters:
first (Linearization) – First curve being intersected.
second (Linearization) – Second curve being intersected.
intersections (list) – A list of existing intersections.
- Raises:
ValueError – If
firstandsecondboth have linearization error of0.0(i.e. they are both lines). This is because this function expects the caller to have usedcheck_lines()already.
- bezier.hazmat.geometric_intersection.add_intersection(s, t, intersections)¶
Adds an intersection to list of
intersections.Note
This is a helper for
from_linearized()andendpoint_check(). These functions are used (directly or indirectly) byall_intersections()exclusively, and that function has a Fortran equivalent.Accounts for repeated intersection points. If the intersection has already been found, does nothing.
If
sis below \(2^{-10}\), it will be replaced with1 - sand compared against1 - s'for alls'already inintersections. (Similar iftis below theZERO_THRESHOLD.) This is perfectly “appropriate” since evaluating a Bézier curve requires using bothsand1 - s, so both values are equally relevant.Compares \(\|p - q\|\) to \(\|p\|\) where \(p = (s, t)\) is current candidate intersection (or the “normalized” version, such as \(p = (1 - s, t)\)) and \(q\) is one of the already added intersections. If the difference is below \(2^{-36}\) (i.e.
NEWTON_ERROR_RATIO) then the intersection is considered to be duplicate.
- bezier.hazmat.geometric_intersection.endpoint_check(first, node_first, s, second, node_second, t, intersections)¶
Check if curve endpoints are identical.
Note
This is a helper for
tangent_bbox_intersection(). These functions are used (directly or indirectly) byall_intersections()exclusively, and that function has a Fortran equivalent.- Parameters:
first (SubdividedCurve) – First curve being intersected (assumed in \(\mathbf{R}^2\)).
node_first (numpy.ndarray) – 1D
2-array, one of the endpoints offirst.s (float) – The parameter corresponding to
node_first, so expected to be one of0.0or1.0.second (SubdividedCurve) – Second curve being intersected (assumed in \(\mathbf{R}^2\)).
node_second (numpy.ndarray) – 1D
2-array, one of the endpoints ofsecond.t (float) – The parameter corresponding to
node_second, so expected to be one of0.0or1.0.intersections (list) – A list of already encountered intersections. If these curves intersect at their tangency, then those intersections will be added to this list.
- bezier.hazmat.geometric_intersection.tangent_bbox_intersection(first, second, intersections)¶
Check if two curves with tangent bounding boxes intersect.
Note
This is a helper for
intersect_one_round(). These functions are used (directly or indirectly) byall_intersections()exclusively, and that function has a Fortran equivalent.If the bounding boxes are tangent, intersection can only occur along that tangency.
If the curve is not a line, the only way the curve can touch the bounding box is at the endpoints. To see this, consider the component
\[x(s) = \sum_j W_j x_j.\]Since \(W_j > 0\) for \(s \in \left(0, 1\right)\), if there is some \(k\) with \(x_k < M = \max x_j\), then for any interior \(s\)
\[x(s) < \sum_j W_j M = M.\]If all \(x_j = M\), then \(B(s)\) falls on the line \(x = M\). (A similar argument holds for the other three component-extrema types.)
Note
This function assumes callers will not pass curves that can be linearized / are linear. In
all_intersections(), curves are pre-processed to do any linearization before the subdivision / intersection process begins.- Parameters:
first (SubdividedCurve) – First curve being intersected (assumed in \(\mathbf{R}^2\)).
second (SubdividedCurve) – Second curve being intersected (assumed in \(\mathbf{R}^2\)).
intersections (list) – A list of already encountered intersections. If these curves intersect at their tangency, then those intersections will be added to this list.
- bezier.hazmat.geometric_intersection.bbox_line_intersect(nodes, line_start, line_end)¶
Determine intersection of a bounding box and a line.
We do this by first checking if either the start or end node of the segment are contained in the bounding box. If they aren’t, then checks if the line segment intersects any of the four sides of the bounding box.
Note
This function is “half-finished”. It makes no distinction between “tangent” intersections of the box and segment and other types of intersection. However, the distinction is worthwhile, so this function should be “upgraded” at some point.
- Parameters:
nodes (numpy.ndarray) – Points (
2 x N) that determine a bounding box.line_start (numpy.ndarray) – Beginning of a line segment (1D
2-array).line_end (numpy.ndarray) – End of a line segment (1D
2-array).
- Returns:
Enum from
BoxIntersectionTypeindicating the type of bounding box intersection.- Return type:
- bezier.hazmat.geometric_intersection.intersect_one_round(candidates, intersections)¶
Perform one step of the intersection process.
Note
This is a helper for
all_intersections()and that function has a Fortran equivalent.Checks if the bounding boxes of each pair in
candidatesintersect. If the bounding boxes do not intersect, the pair is discarded. Otherwise, the pair is “accepted”. Then we attempt to linearize each curve in an “accepted” pair and track the overall linearization error for every curve encountered.- Parameters:
candidates (
Unionlist,itertools.chain) – An iterable of pairs of curves (or linearized curves).intersections (list) – A list of already encountered intersections. If any intersections can be readily determined during this round of subdivision, then they will be added to this list.
- Returns:
Returns a list of the next round of
candidates.- Return type:
- bezier.hazmat.geometric_intersection.prune_candidates(candidates)¶
Reduce number of candidate intersection pairs.
Note
This is a helper for
all_intersections().Uses more strict bounding box intersection predicate by forming the actual convex hull of each candidate curve segment and then checking if those convex hulls collide.
- Parameters:
candidates (
ListUnionSubdividedCurve,Linearization) – An iterable of pairs of curves (or linearized curves).- Returns:
A pruned list of curve pairs.
- Return type:
- bezier.hazmat.geometric_intersection.make_same_degree(nodes1, nodes2)¶
Degree-elevate a curve so two curves have matching degree.
- Parameters:
nodes1 (numpy.ndarray) – Set of control points for a Bézier curve.
nodes2 (numpy.ndarray) – Set of control points for a Bézier curve.
- Returns:
The potentially degree-elevated nodes passed in.
- Return type:
- bezier.hazmat.geometric_intersection.coincident_parameters(nodes1, nodes2)¶
Check if two Bézier curves are coincident.
Does so by projecting each segment endpoint onto the other curve
\[\begin{split}B_1(s_0) = B_2(0) \\ B_1(s_m) = B_2(1) \\ B_1(0) = B_2(t_0) \\ B_1(1) = B_2(t_n)\end{split}\]and then finding the “shared interval” where both curves are defined. If such an interval can’t be found (e.g. if one of the endpoints can’t be located on the other curve), returns
None.If such a “shared interval” does exist, then this will specialize each curve onto that shared interval and check if the new control points agree.
- Parameters:
nodes1 (numpy.ndarray) – Set of control points for a Bézier curve.
nodes2 (numpy.ndarray) – Set of control points for a Bézier curve.
- Returns:
A
2 x 2array of parameters where the two coincident curves meet. If they are not coincident, returnsNone.- Return type:
- bezier.hazmat.geometric_intersection.check_lines(first, second)¶
Checks if two curves are lines and tries to intersect them.
Note
This is a helper for
all_intersections().If they are not lines / not linearized, immediately returns
Falsewith no “return value”.If they are lines, attempts to intersect them (even if they are parallel and share a coincident segment).
- Parameters:
first (
UnionSubdividedCurve,Linearization) – First curve being intersected.second (
UnionSubdividedCurve,Linearization) – Second curve being intersected.
- Returns:
A pair of
Flag indicating if both candidates in the pair are lines.
Optional “result” populated only if both candidates are lines. When this result is populated, it will be a pair of
array of parameters of intersection
flag indicating if the two candidates share a coincident segment
- Return type:
- bezier.hazmat.geometric_intersection.all_intersections(nodes_first, nodes_second)¶
Find the points of intersection among a pair of curves.
Note
There is also a Fortran implementation of this function, which will be used if it can be built.
Note
This assumes both curves are in \(\mathbf{R}^2\), but does not explicitly check this. However, functions used here will fail if that assumption fails, e.g.
bbox_intersect()andnewton_refine().- Parameters:
nodes_first (numpy.ndarray) – Control points of a curve to be intersected with
nodes_second.nodes_second (numpy.ndarray) – Control points of a curve to be intersected with
nodes_first.
- Returns:
An array and a flag:
A
2 x Narray of intersection parameters. Each row contains a pair of values \(s\) and \(t\) (each in \(\left[0, 1\right]\)) such that the curves intersect: \(B_1(s) = B_2(t)\).Flag indicating if the curves are coincident.
- Return type:
- Raises:
ValueError – If the subdivision iteration does not terminate before exhausting the maximum number of subdivisions.
NotImplementedError – If the subdivision process picks up too many candidate pairs. This typically indicates tangent curves or coincident curves (though there are mitigations for those cases in place).
- class bezier.hazmat.geometric_intersection.BoxIntersectionType¶
Bases:
objectEnum representing all possible bounding box intersections.
Note
This class would be more “correct” as an
enum.Enum, but it we keep the values integers to make interfacing with Fortran easier.- INTERSECTION = 0¶
Bounding boxes overlap with positive area.
- TANGENT = 1¶
Bounding boxes are tangent but do not overlap.
- DISJOINT = 2¶
Bounding boxes do not intersect or touch.
- class bezier.hazmat.geometric_intersection.SubdividedCurve(nodes, original_nodes, start=0.0, end=1.0)¶
Bases:
objectA data wrapper for a Bézier curve
To be used for intersection algorithm via repeated subdivision, where the
startandendparameters must be tracked.- Parameters:
nodes (numpy.ndarray) – The control points of the current subdivided curve
original_nodes (numpy.ndarray) – The control points of the original curve used to define the current one (before subdivision began).
start (
Optionalfloat) – The start parameter after subdivision.
- nodes¶
- original_nodes¶
- start¶
- end¶
- subdivide()¶
Split the curve into a left and right half.
See
Curve.subdivide()for more information.- Returns:
The left and right sub-curves.
- Return type:
- class bezier.hazmat.geometric_intersection.Linearization(curve, error)¶
Bases:
objectA linearization of a curve.
This class is provided as a stand-in for a curve, so it provides a similar interface.
- Parameters:
curve (SubdividedCurve) – A curve that is linearized.
error (float) – The linearization error. Expected to have been computed via
linearization_error().
- curve¶
The curve that this linearization approximates.
- Type:
- start_node¶
The 1D start vector of this linearization.
- Type:
- end_node¶
The 1D end vector of this linearization.
- Type:
- subdivide()¶
Do-nothing method to match the
Curveinterface.- Returns:
List of all subdivided parts, which is just the current object.
- Return type:
- classmethod from_shape(shape)¶
Try to linearize a curve (or an already linearized curve).
- Parameters:
shape (
UnionSubdividedCurve,Linearization) – A curve or an already linearized curve.- Returns:
The (potentially linearized) curve.
- Return type:
- bezier.hazmat.geometric_intersection.self_intersections(nodes)¶
Determine the self-intersections of a planar Bézier curve.
See: https://doi.org/10.1016/0166-3615(89)90072-9
- Parameters:
nodes (numpy.ndarray) – The nodes in the curve.
- Returns:
Pairs of parameters along the curve where self-intersections occur (as a 2D array).
- Return type: