bezier.hazmat.curve_helpers module

Pure Python implementations of helper methods for Bézier curves.

bezier.hazmat.curve_helpers.make_subdivision_matrices(degree)

Make the matrix used to subdivide a curve.

Note

This is a helper for subdivide_nodes(). It does not have a Fortran speedup because it is only used by a function which has a Fortran speedup.

Parameters:: degree (int) – The degree of the curve.
Returns:: The matrices used to convert the nodes into left and right nodes, respectively.
Return type:: Tuplenumpy.ndarray, numpy.ndarray

bezier.hazmat.curve_helpers.subdivide_nodes(nodes)

Subdivide a curve into two sub-curves.

Does so by taking the unit interval (i.e. the domain of the curve) and splitting it into two sub-intervals by splitting down the middle.

Note

There is also a Fortran implementation of this function, which will be used if it can be built.

Parameters:: nodes (numpy.ndarray) – The nodes defining a Bézier curve.
Returns:: The nodes for the two sub-curves.
Return type:: Tuplenumpy.ndarray, numpy.ndarray

bezier.hazmat.curve_helpers.evaluate_multi(nodes, s_vals)

Computes multiple points along a curve.

Note

There is also a Fortran implementation of this function, which will be used if it can be built.

Parameters:

nodes (numpy.ndarray) – The nodes defining a curve.
s_vals (numpy.ndarray) – Parameters along the curve (as a 1D array).

Returns:

The evaluated points on the curve as a two dimensional NumPy array, with the columns corresponding to each s value and the rows to the dimension.

Return type:

numpy.ndarray

bezier.hazmat.curve_helpers.evaluate_multi_vs(nodes, lambda1, lambda2)

Evaluates a Bézier type-function.

Of the form

\[B(\lambda_1, \lambda_2) = \sum_j \binom{n}{j} \lambda_1^{n - j} \lambda_2^j \cdot v_j\]

for some set of vectors \(v_j\) given by nodes.

Does so via a modified Horner’s method (the VS Algorithm) for each pair of values in lambda1 and lambda2.

\[\begin{split}\begin{align*} w_0 &= \lambda_1 v_0 \\ w_j &= \lambda_1 \left[w_{j - 1} + \binom{n}{j} \lambda_2^j v_j\right] \\ w_n &= w_{n - 1} + \lambda_2^n v_n \\ B(\lambda_1, \lambda_2) &= w_n \end{align*}\end{split}\]

Additionally, binomial coefficients are computed by utilizing the fact that \(\binom{n}{j} = \binom{n}{j - 1} \frac{n - j + 1}{j}\).

Parameters:

nodes (numpy.ndarray) – The nodes defining a curve.
lambda1 (numpy.ndarray) – Parameters along the curve (as a 1D array).
lambda2 (numpy.ndarray) – Parameters along the curve (as a 1D array). Typically we have lambda1 + lambda2 == 1.

Returns:

The evaluated points as a two dimensional NumPy array, with the columns corresponding to each pair of parameter values and the rows to the dimension.

Return type:

numpy.ndarray

bezier.hazmat.curve_helpers.evaluate_multi_de_casteljau(nodes, lambda1, lambda2)

Evaluates a Bézier type-function.

Of the form

\[B(\lambda_1, \lambda_2) = \sum_j \binom{n}{j} \lambda_1^{n - j} \lambda_2^j \cdot v_j\]

for some set of vectors \(v_j\) given by nodes.

Does so via the de Castljau algorithm:

\[\begin{split}\begin{align*} v_j^{(n)} &= v_j \\ v_j^{(k)} &= \lambda_1 \cdot v_j^{(k + 1)} + \lambda_2 \cdot v_{j + 1}^{(k + 1)} \\ B(\lambda_1, \lambda_2) &= v_0^{(0)} \end{align*}\end{split}\]

Parameters:

nodes (numpy.ndarray) – The nodes defining a curve.
lambda1 (numpy.ndarray) – Parameters along the curve (as a 1D array).
lambda2 (numpy.ndarray) – Parameters along the curve (as a 1D array). Typically we have lambda1 + lambda2 == 1.

Returns:

The evaluated points as a two dimensional NumPy array, with the columns corresponding to each pair of parameter values and the rows to the dimension.

Return type:

numpy.ndarray

bezier.hazmat.curve_helpers.evaluate_multi_barycentric(nodes, lambda1, lambda2)

Evaluates a Bézier type-function.

Of the form

\[B(\lambda_1, \lambda_2) = \sum_j \binom{n}{j} \lambda_1^{n - j} \lambda_2^j \cdot v_j\]

for some set of vectors \(v_j\) given by nodes. This uses the more efficient evaluate_multi_vs() until degree 55, at which point \(\binom{55}{26}\) and other coefficients cannot be computed exactly. For degree 55 and higher, the classical de Casteljau algorithm will be used via evaluate_multi_de_casteljau().

Note

There is also a Fortran implementation of this function, which will be used if it can be built.

Parameters:

nodes (numpy.ndarray) – The nodes defining a curve.
lambda1 (numpy.ndarray) – Parameters along the curve (as a 1D array).
lambda2 (numpy.ndarray) – Parameters along the curve (as a 1D array). Typically we have lambda1 + lambda2 == 1.

Returns:

The evaluated points as a two dimensional NumPy array, with the columns corresponding to each pair of parameter values and the rows to the dimension.

Return type:

numpy.ndarray

bezier.hazmat.curve_helpers.vec_size(nodes, s_val)

Compute \(\|B(s)\|_2\).

Note

This is a helper for compute_length() and does not have a Fortran speedup.

Intended to be used with functools.partial() to fill in the value of nodes and create a callable that only accepts s_val.

Parameters:

nodes (numpy.ndarray) – The nodes defining a curve.
s_val (float) – Parameter to compute \(B(s)\).

Returns:

The norm of \(B(s)\).

Return type:

float

bezier.hazmat.curve_helpers.compute_length(nodes)

Approximately compute the length of a curve.

If degree is \(n\), then the Hodograph curve \(B'(s)\) is degree \(d = n - 1\). Using this curve, we approximate the integral:

\[\int_{B\left(\left[0, 1\right]\right)} 1 \, d\mathbf{x} = \int_0^1 \left\lVert B'(s) \right\rVert_2 \, ds\]

using QUADPACK (via SciPy).

Note

There is also a Fortran implementation of this function, which will be used if it can be built.

Parameters:: nodes (numpy.ndarray) – The nodes defining a curve.
Returns:: The length of the curve.
Return type:: float
Raises:: ValueError – If nodes has zero columns.

bezier.hazmat.curve_helpers.elevate_nodes(nodes)

Degree-elevate a Bézier curve.

Does this by converting the current nodes \(v_0, \ldots, v_n\) to new nodes \(w_0, \ldots, w_{n + 1}\) where

\[\begin{split}\begin{align*} w_0 &= v_0 \\ w_j &= \frac{j}{n + 1} v_{j - 1} + \frac{n + 1 - j}{n + 1} v_j \\ w_{n + 1} &= v_n \end{align*}\end{split}\]

Note

There is also a Fortran implementation of this function, which will be used if it can be built.

Parameters:: nodes (numpy.ndarray) – The nodes defining a curve.
Returns:: The nodes of the degree-elevated curve.
Return type:: numpy.ndarray

bezier.hazmat.curve_helpers.de_casteljau_one_round(nodes, lambda1, lambda2)

Perform one round of de Casteljau’s algorithm.

Note

This is a helper for specialize_curve(). It does not have a Fortran speedup because it is only used by a function which has a Fortran speedup.

The weights are assumed to sum to one.

Parameters:

nodes (numpy.ndarray) – Control points for a curve.
lambda1 (float) – First barycentric weight on interval.
lambda2 (float) – Second barycentric weight on interval.

Returns:

The nodes for a “blended” curve one degree lower.

Return type:

numpy.ndarray

bezier.hazmat.curve_helpers.specialize_curve(nodes, start, end)

Specialize a curve to a re-parameterization

Note

This assumes the curve is degree 1 or greater but doesn’t check.

Note

There is also a Fortran implementation of this function, which will be used if it can be built.

Parameters:

nodes (numpy.ndarray) – Control points for a curve.
start (float) – The start point of the interval we are specializing to.
end (float) – The end point of the interval we are specializing to.

Returns:

The control points for the specialized curve.

Return type:

numpy.ndarray

bezier.hazmat.curve_helpers.evaluate_hodograph(s, nodes)

Evaluate the Hodograph curve at a point \(s\).

The Hodograph (first derivative) of a Bézier curve degree \(d = n - 1\) and is given by

\[B'(s) = n \sum_{j = 0}^{d} \binom{d}{j} s^j (1 - s)^{d - j} \cdot \Delta v_j\]

where each forward difference is given by \(\Delta v_j = v_{j + 1} - v_j\).

Note

There is also a Fortran implementation of this function, which will be used if it can be built.

Parameters:

nodes (numpy.ndarray) – The nodes of a curve.
s (float) – A parameter along the curve at which the Hodograph is to be evaluated.

Returns:

The point on the Hodograph curve (as a two dimensional NumPy array with a single row).

Return type:

numpy.ndarray

bezier.hazmat.curve_helpers.get_curvature(nodes, tangent_vec, s)

Compute the signed curvature of a curve at \(s\).

Computed via

\[\frac{B'(s) \times B''(s)}{\left\lVert B'(s) \right\rVert_2^3}\]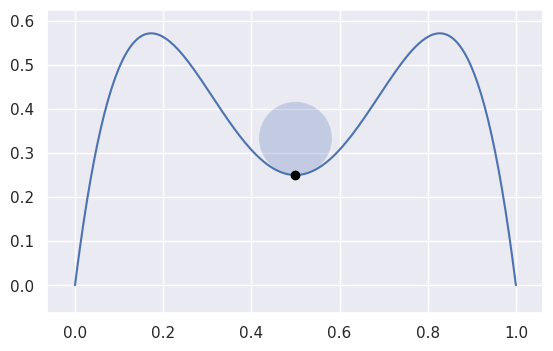

>>> import numpy as np
>>> nodes = np.asfortranarray([
...     [1.0, 0.75,  0.5, 0.25, 0.0],
...     [0.0, 2.0 , -2.0, 2.0 , 0.0],
... ])
>>> s = 0.5
>>> tangent_vec = evaluate_hodograph(s, nodes)
>>> tangent_vec
array([[-1.],
       [ 0.]])
>>> curvature = get_curvature(nodes, tangent_vec, s)
>>> float(curvature)
-12.0

Note

There is also a Fortran implementation of this function, which will be used if it can be built.

Parameters:

nodes (numpy.ndarray) – The nodes of a curve.
tangent_vec (numpy.ndarray) – The already computed value of \(B'(s)\)
s (float) – The parameter value along the curve.

Returns:

The signed curvature.

Return type:

float

bezier.hazmat.curve_helpers.newton_refine(nodes, point, s)

Refine a solution to \(B(s) = p\) using Newton’s method.

Computes updates via

\[\mathbf{0} \approx \left(B\left(s_{\ast}\right) - p\right) + B'\left(s_{\ast}\right) \Delta s\]

For example, consider the curve

\[\begin{split}B(s) = \left[\begin{array}{c} 0 \\ 0 \end{array}\right] (1 - s)^2 + \left[\begin{array}{c} 1 \\ 2 \end{array}\right] 2 (1 - s) s + \left[\begin{array}{c} 3 \\ 1 \end{array}\right] s^2\end{split}\]

and the point \(B\left(\frac{1}{4}\right) = \frac{1}{16} \left[\begin{array}{c} 9 \\ 13 \end{array}\right]\).

Starting from the wrong point \(s = \frac{3}{4}\), we have

\[\begin{split}\begin{align*} p - B\left(\frac{1}{2}\right) &= -\frac{1}{2} \left[\begin{array}{c} 3 \\ 1 \end{array}\right] \\ B'\left(\frac{1}{2}\right) &= \frac{1}{2} \left[\begin{array}{c} 7 \\ -1 \end{array}\right] \\ \Longrightarrow \frac{1}{4} \left[\begin{array}{c c} 7 & -1 \end{array}\right] \left[\begin{array}{c} 7 \\ -1 \end{array}\right] \Delta s &= -\frac{1}{4} \left[\begin{array}{c c} 7 & -1 \end{array}\right] \left[\begin{array}{c} 3 \\ 1 \end{array}\right] \\ \Longrightarrow \Delta s &= -\frac{2}{5} \end{align*}\end{split}\]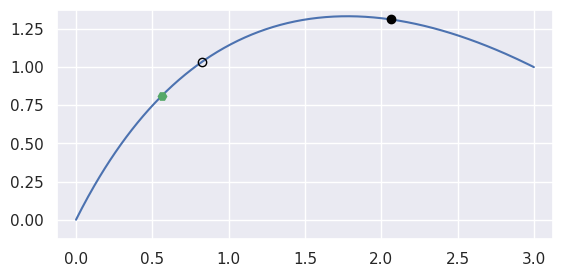

>>> import bezier
>>> nodes = np.asfortranarray([
...     [0.0, 1.0, 3.0],
...     [0.0, 2.0, 1.0],
... ])
>>> curve = bezier.Curve(nodes, degree=2)
>>> point = curve.evaluate(0.25)
>>> point
array([[0.5625],
       [0.8125]])
>>> s = 0.75
>>> new_s = newton_refine(nodes, point, s)
>>> float(5 * (new_s - s))
-2.0

On curves that are not “valid” (i.e. \(B(s)\) is not injective with non-zero gradient), Newton’s method may break down and converge linearly:

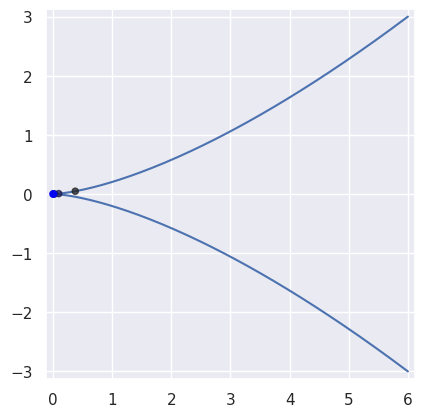
../../_images/newton_refine_curve_cusp.png

>>> nodes = np.asfortranarray([
...     [ 6.0, -2.0, -2.0, 6.0],
...     [-3.0,  3.0, -3.0, 3.0],
... ])
>>> curve = bezier.Curve(nodes, degree=3)
>>> expected = 0.5
>>> point = curve.evaluate(expected)
>>> point
array([[0.],
       [0.]])
>>> s_vals = [0.625, None, None, None, None, None]
>>> float(np.log2(abs(expected - s_vals[0])))
-3.0
>>> s_vals[1] = newton_refine(nodes, point, s_vals[0])
>>> float(np.log2(abs(expected - s_vals[1])))
-3.983...
>>> s_vals[2] = newton_refine(nodes, point, s_vals[1])
>>> float(np.log2(abs(expected - s_vals[2])))
-4.979...
>>> s_vals[3] = newton_refine(nodes, point, s_vals[2])
>>> float(np.log2(abs(expected - s_vals[3])))
-5.978...
>>> s_vals[4] = newton_refine(nodes, point, s_vals[3])
>>> float(np.log2(abs(expected - s_vals[4])))
-6.978...
>>> s_vals[5] = newton_refine(nodes, point, s_vals[4])
>>> float(np.log2(abs(expected - s_vals[5])))
-7.978...

Due to round-off, the Newton process terminates with an error that is not close to machine precision \(\varepsilon\) when \(\Delta s = 0\).

>>> s_vals = [0.625]
>>> new_s = newton_refine(nodes, point, s_vals[-1])
>>> while new_s not in s_vals:
...     s_vals.append(new_s)
...     new_s = newton_refine(nodes, point, s_vals[-1])
...
>>> terminal_s = s_vals[-1]
>>> bool(terminal_s == newton_refine(nodes, point, terminal_s))
True
>>> 2.0**(-31) <= float(abs(terminal_s - 0.5)) <= 2.0**(-28)
True

Due to round-off near the cusp, the final error resembles \(\sqrt{\varepsilon}\) rather than machine precision as expected.

Note

There is also a Fortran implementation of this function, which will be used if it can be built.

Parameters:

nodes (numpy.ndarray) – The nodes defining a Bézier curve.
point (numpy.ndarray) – A point on the curve.
s (float) – An “almost” solution to \(B(s) = p\).

Returns:

The updated value \(s + \Delta s\).

Return type:

float

bezier.hazmat.curve_helpers.locate_point(nodes, point)

Locate a point on a curve.

Does so by recursively subdividing the curve and rejecting sub-curves with bounding boxes that don’t contain the point. After the sub-curves are sufficiently small, uses Newton’s method to zoom in on the parameter value.

Note

This assumes, but does not check, that point is D x 1, where D is the dimension that curve is in.

Note

There is also a Fortran implementation of this function, which will be used if it can be built.

Parameters:

nodes (numpy.ndarray) – The nodes defining a Bézier curve.
point (numpy.ndarray) – The point to locate.

Returns:

The parameter value (\(s\)) corresponding to point or None if the point is not on the curve.

Return type:

Optionalfloat

Raises:

ValueError – If the standard deviation of the remaining start / end parameters among the subdivided intervals exceeds a given threshold (e.g. \(2^{-20}\)).

bezier.hazmat.curve_helpers.reduce_pseudo_inverse(nodes)

Performs degree-reduction for a Bézier curve.

Does so by using the pseudo-inverse of the degree elevation operator (which is overdetermined).

Note

There is also a Fortran implementation of this function, which will be used if it can be built.

Parameters:: nodes (numpy.ndarray) – The nodes in the curve.
Returns:: The reduced nodes.
Return type:: numpy.ndarray
Raises:: UnsupportedDegree – If the degree is not 1, 2, 3 or 4.

bezier.hazmat.curve_helpers.projection_error(nodes, projected)

Compute the error between nodes and the projected nodes.

Note

This is a helper for maybe_reduce(), which is in turn a helper for full_reduce(). Hence there is no corresponding Fortran speedup.

For now, just compute the relative error in the Frobenius norm. But, we may wish to consider the error per row / point instead.

Parameters:

nodes (numpy.ndarray) – Nodes in a curve.
projected (numpy.ndarray) – The nodes projected into the space of degree-elevated nodes.

Returns:

The relative error.

Return type:

float

bezier.hazmat.curve_helpers.maybe_reduce(nodes)

Reduce nodes in a curve if they are degree-elevated.

Note

This is a helper for full_reduce(). Hence there is no corresponding Fortran speedup.

We check if the nodes are degree-elevated by projecting onto the space of degree-elevated curves of the same degree, then comparing to the projection. We form the projection by taking the corresponding (right) elevation matrix \(E\) (from one degree lower) and forming \(E^T \left(E E^T\right)^{-1} E\).

Parameters:: nodes (numpy.ndarray) – The nodes in the curve.
Returns:: Pair of values. The first indicates if the nodes were reduced. The second is the resulting nodes, either the reduced ones or the original passed in.
Return type:: Tuplebool, numpy.ndarray
Raises:: UnsupportedDegree – If the curve is degree 5 or higher.

bezier.hazmat.curve_helpers.full_reduce(nodes)

Apply degree reduction to nodes until it can no longer be reduced.

Note

There is also a Fortran implementation of this function, which will be used if it can be built.

Parameters:: nodes (numpy.ndarray) – The nodes in the curve.
Returns:: The fully degree-reduced nodes.
Return type:: numpy.ndarray

bezier.hazmat.curve_helpers.discrete_turning_angle(nodes)

Determine the absolute sum of Bézier node angles.

Note

This assumes, but does not check, that nodes is 2 x N.

For the set of vectors \(v_j\) given by nodes, the discrete angles \(\theta_j\) at each internal node is given by

\[\left(v_{j} - v_{j - 1}\right) \cdot \left(v_{j + 1} - v_{j}\right) = \| v_{j} - v_{j - 1} \|_2 \| v_{j + 1} - v_{j} \|_2 \cos \theta_j\]

and the discrete turning angle is \(\sum_{j} \left|\theta_j\right|\). This approximates the exact turning angle

\[\int_0^1 \left|\theta'(s)\right| \, ds.\]

This is done by considering how the angle of \(B'(s) = \left[x'(s), y'(s)\right]^T\) changes in small intervals in the parameter space; where the angle is \(\theta(s) = \arctan(y'(s) / x'(s))\). Computing \(\theta(s + ds) - \theta(s)\) as \(ds \longrightarrow 0\) leaves us with the signed angle change

\[\theta'(s) = \frac{y''(s) x'(s) - x''(s) y'(s)}{x'(s)^2 + y'(s)^2}.\]

Parameters:: nodes (numpy.ndarray) – The nodes in the curve.
Returns:: The (discrete) turning angle.
Return type:: float