Curve-Curve Intersection¶
The problem of intersecting two curves is a difficult one
in computational geometry. The Curve.intersect() method (when using
the GEOMETRIC strategy) uses a combination of
curve subdivision, bounding box intersection, and curve approximation (by
lines) to find intersections.
Curve-Line Intersection¶
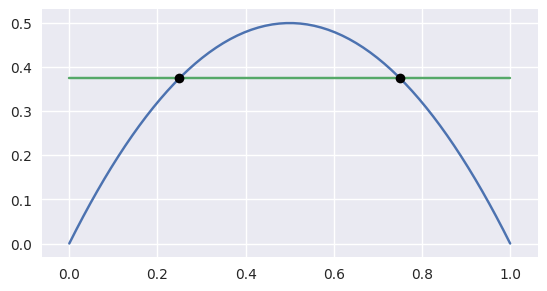
>>> nodes1 = np.asfortranarray([
... [0.0, 0.5, 1.0],
... [0.0, 1.0, 0.0],
... ])
>>> curve1 = bezier.Curve(nodes1, degree=2)
>>> nodes2 = np.asfortranarray([
... [0.0 , 1.0 ],
... [0.375, 0.375],
... ])
>>> curve2 = bezier.Curve(nodes2, degree=1)
>>> intersections = curve1.intersect(curve2)
>>> intersections
array([[0.25, 0.75],
[0.25, 0.75]])
>>> s_vals = np.asfortranarray(intersections[0, :])
>>> curve1.evaluate_multi(s_vals)
array([[0.25 , 0.75 ],
[0.375, 0.375]])
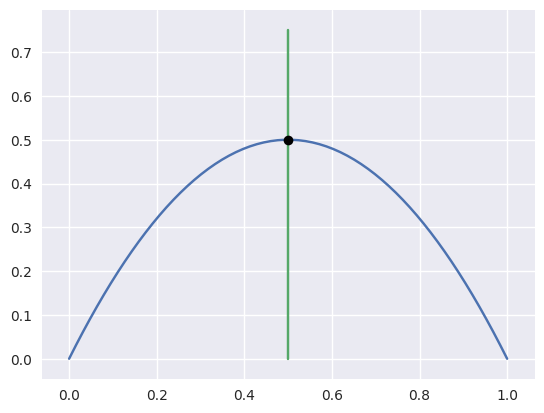
>>> nodes1 = np.asfortranarray([
... [0.0, 0.5, 1.0],
... [0.0, 1.0, 0.0],
... ])
>>> curve1 = bezier.Curve(nodes1, degree=2)
>>> nodes2 = np.asfortranarray([
... [0.5, 0.5 ],
... [0.0, 0.75],
... ])
>>> curve2 = bezier.Curve(nodes2, degree=1)
>>> intersections = curve1.intersect(curve2)
>>> intersections
array([[0.5 ],
[0.6666...]])
>>> s_vals = np.asfortranarray(intersections[0, :])
>>> curve1.evaluate_multi(s_vals)
array([[0.5],
[0.5]])
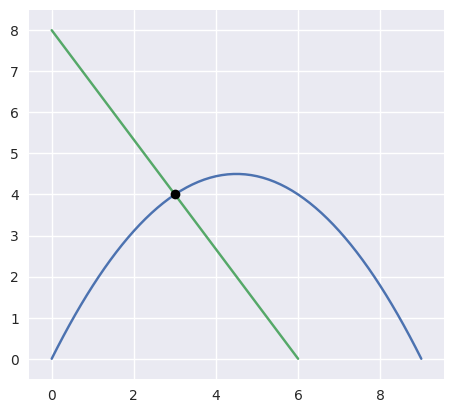
>>> nodes1 = np.asfortranarray([
... [0.0, 4.5, 9.0],
... [0.0, 9.0, 0.0],
... ])
>>> curve1 = bezier.Curve(nodes1, degree=2)
>>> nodes2 = np.asfortranarray([
... [0.0, 6.0],
... [8.0, 0.0],
... ])
>>> curve2 = bezier.Curve(nodes2, degree=1)
>>> intersections = curve1.intersect(curve2)
>>> intersections
array([[0.3333...],
[0.5 ]])
>>> s_vals = np.asfortranarray(intersections[0, :])
>>> curve1.evaluate_multi(s_vals)
array([[3.],
[4.]])
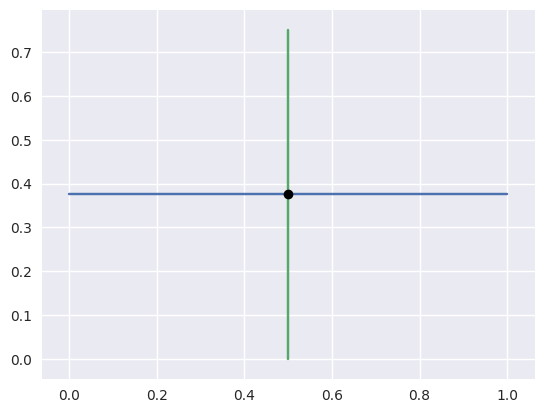
>>> nodes1 = np.asfortranarray([
... [0.0 , 1.0 ],
... [0.375, 0.375],
... ])
>>> curve1 = bezier.Curve(nodes1, degree=1)
>>> nodes2 = np.asfortranarray([
... [0.5, 0.5 ],
... [0.0, 0.75],
... ])
>>> curve2 = bezier.Curve(nodes2, degree=1)
>>> intersections = curve1.intersect(curve2)
>>> intersections
array([[0.5],
[0.5]])
>>> s_vals = np.asfortranarray(intersections[0, :])
>>> curve1.evaluate_multi(s_vals)
array([[0.5 ],
[0.375]])
>>> nodes1 = np.asfortranarray([
... [-1.0, 0.5, 0.0],
... [ 1.0, 0.5, 2.0],
... ])
>>> curve1 = bezier.Curve(nodes1, degree=2)
>>> nodes2 = np.asfortranarray([
... [0.5, -0.25],
... [0.5, 1.25],
... ])
>>> curve2 = bezier.Curve(nodes2, degree=1)
>>> intersections = curve1.intersect(curve2)
>>> intersections
array([[0.5 ],
[0.6666...]])
>>> s_vals = np.asfortranarray(intersections[0, :])
>>> curve1.evaluate_multi(s_vals)
array([[0.],
[1.]])
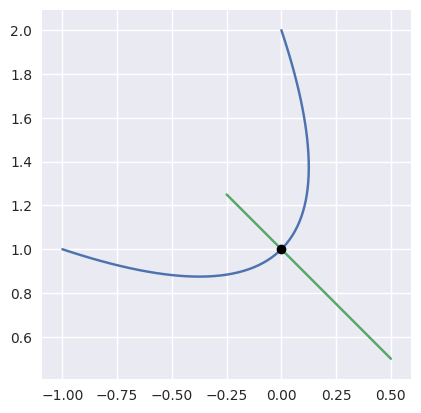
Curved Intersections¶
For curves which intersect at exact floating point numbers, we can typically compute the intersection with zero error:
>>> nodes1 = np.asfortranarray([
... [0.0, 0.5, 1.0],
... [0.0, 1.0, 0.0],
... ])
>>> curve1 = bezier.Curve(nodes1, degree=2)
>>> nodes2 = np.asfortranarray([
... [0.0 , 0.5 , 1.0 ],
... [0.75, -0.25, 0.75],
... ])
>>> curve2 = bezier.Curve(nodes2, degree=2)
>>> intersections = curve1.intersect(curve2)
>>> intersections
array([[0.25, 0.75],
[0.25, 0.75]])
>>> s_vals = np.asfortranarray(intersections[0, :])
>>> curve1.evaluate_multi(s_vals)
array([[0.25 , 0.75 ],
[0.375, 0.375]])
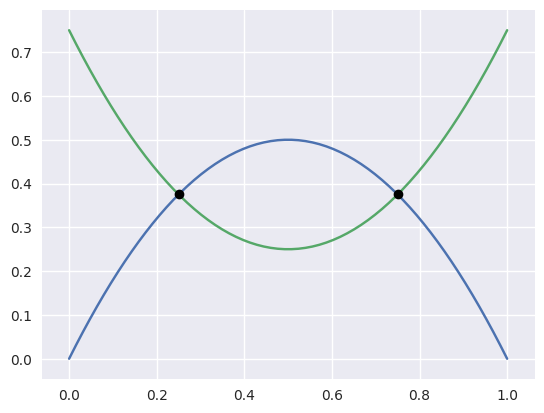
>>> nodes1 = np.asfortranarray([
... [0.0, 1.5, 3.0],
... [0.0, 3.0, 0.0],
... ])
>>> curve1 = bezier.Curve(nodes1, degree=2)
>>> nodes2 = np.asfortranarray([
... [3.0, 2.625 , -0.75 ],
... [1.5, -0.90625, 2.4375],
... ])
>>> curve2 = bezier.Curve(nodes2, degree=2)
>>> intersections = curve1.intersect(curve2)
>>> intersections
array([[0.25 , 0.875],
[0.75 , 0.25 ]])
>>> s_vals = np.asfortranarray(intersections[0, :])
>>> curve1.evaluate_multi(s_vals)
array([[0.75 , 2.625 ],
[1.125 , 0.65625]])
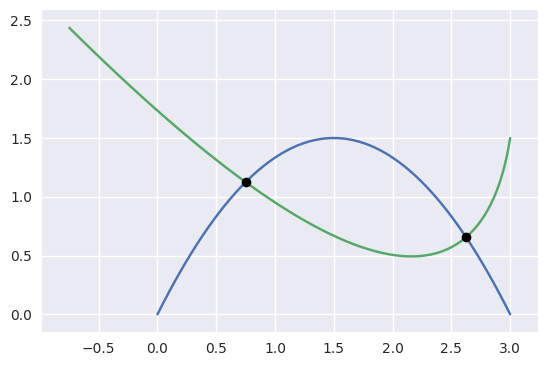
>>> nodes1 = np.asfortranarray([
... [0.0, 0.375, 0.75 ],
... [0.0, 0.75 , 0.375],
... ])
>>> curve1 = bezier.Curve(nodes1, degree=2)
>>> nodes2 = np.asfortranarray([
... [0.25 , 0.625 , 1.0 ],
... [0.5625, 0.1875, 0.9375],
... ])
>>> curve2 = bezier.Curve(nodes2, degree=2)
>>> intersections = curve1.intersect(curve2)
>>> intersections
array([[0.5 , 0.8333...],
[0.16666..., 0.5 ]])
>>> s_vals = np.asfortranarray(intersections[0, :])
>>> curve1.evaluate_multi(s_vals)
array([[0.375 , 0.625 ],
[0.46875, 0.46875]])
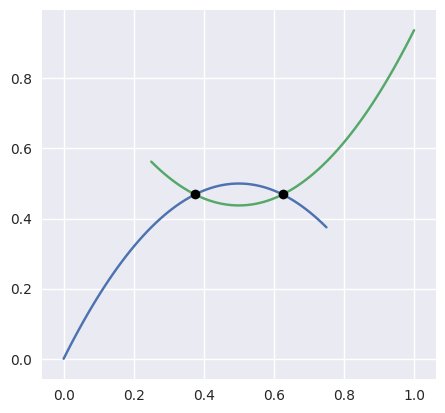
Even for curves which don’t intersect at exact floating point numbers, we can compute the intersection to machine precision:
>>> nodes1 = np.asfortranarray([
... [0.0, 0.5, 1.0],
... [0.0, 1.0, 0.0],
... ])
>>> curve1 = bezier.Curve(nodes1, degree=2)
>>> nodes2 = np.asfortranarray([
... [1.125, 0.625, 0.125],
... [0.5 , -0.5 , 0.5 ],
... ])
>>> curve2 = bezier.Curve(nodes2, degree=2)
>>> intersections = curve1.intersect(curve2)
>>> sq31 = np.sqrt(31.0)
>>> expected_ints = np.asfortranarray([
... [9 - sq31, 9 + sq31],
... [9 + sq31, 9 - sq31],
... ]) / 16.0
>>> max_err = np.max(np.abs(intersections - expected_ints))
>>> binary_exponent(max_err) <= -53
True
>>> s_vals = np.asfortranarray(intersections[0, :])
>>> points = curve1.evaluate_multi(s_vals)
>>> expected_pts = np.asfortranarray([
... [36 - 4 * sq31, 36 + 4 * sq31],
... [ 16 + sq31, 16 - sq31 ],
... ]) / 64.0
>>> max_err = np.max(np.abs(points - expected_pts))
>>> binary_exponent(max_err)
-54
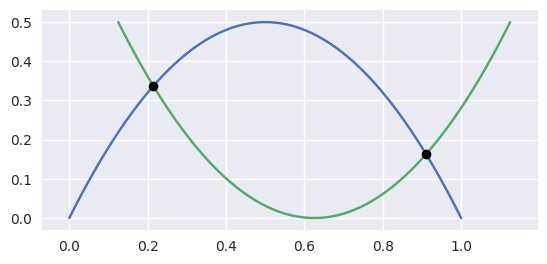
>>> nodes1 = np.asfortranarray([
... [0.0, 0.5, 1.0],
... [0.0, 1.0, 0.0],
... ])
>>> curve1 = bezier.Curve(nodes1, degree=2)
>>> nodes2 = np.asfortranarray([
... [0.0 , 0.5 , 1.0 ],
... [0.265625, 0.234375, 0.265625],
... ])
>>> curve2 = bezier.Curve(nodes2, degree=2)
>>> intersections = curve1.intersect(curve2)
>>> sq33 = np.sqrt(33.0)
>>> expected_ints = np.asfortranarray([
... [33 - 4 * sq33, 33 + 4 * sq33],
... [33 - 4 * sq33, 33 + 4 * sq33],
... ]) / 66.0
>>> max_err = np.max(np.abs(intersections - expected_ints))
>>> binary_exponent(max_err)
-54
>>> s_vals = np.asfortranarray(intersections[0, :])
>>> points = curve1.evaluate_multi(s_vals)
>>> expected_pts = np.asfortranarray([
... [33 - 4 * sq33, 33 + 4 * sq33],
... [ 17, 17 ],
... ]) / 66.0
>>> max_err = np.max(np.abs(points - expected_pts))
>>> binary_exponent(max_err)
-54
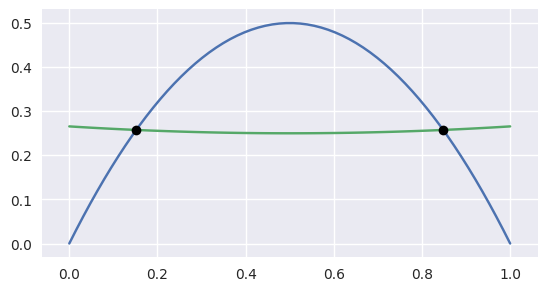
>>> nodes1 = np.asfortranarray([
... [0.0, 0.5, 1.0],
... [0.0, 1.0, 0.0],
... ])
>>> curve1 = bezier.Curve(nodes1, degree=2)
>>> nodes2 = np.asfortranarray([
... [0.0, 0.25, 0.5, 0.75, 1.0],
... [0.0, 2.0 , -2.0, 2.0 , 0.0],
... ])
>>> curve2 = bezier.Curve(nodes2, degree=4)
>>> intersections = curve1.intersect(curve2)
>>> s_vals = np.asfortranarray(intersections[0, :])
>>> points = curve1.evaluate_multi(s_vals)
>>> sq7 = np.sqrt(7.0)
>>> expected_ints = np.asfortranarray([
... [7 - sq7, 7 + sq7, 0, 14],
... [7 - sq7, 7 + sq7, 0, 14],
... ]) / 14.0
>>> max_err = np.max(np.abs(intersections - expected_ints))
>>> binary_exponent(max_err) <= -53
True
>>> expected_pts = np.asfortranarray([
... [7 - sq7, 7 + sq7, 0, 14],
... [ 6, 6, 0, 0 ],
... ]) / 14.0
>>> max_err = np.max(np.abs(points - expected_pts))
>>> binary_exponent(max_err) <= -53
True
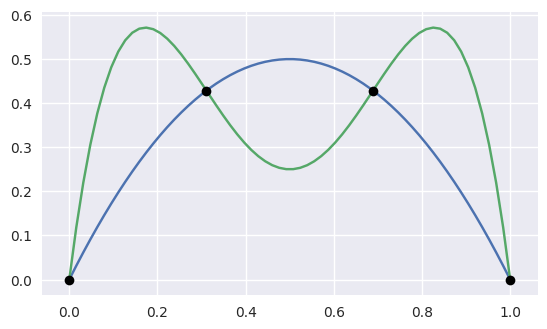
>>> nodes1 = np.asfortranarray([
... [-0.125 , 0.5 , 1.125 ],
... [-0.28125, 1.28125, -0.28125],
... ])
>>> curve1 = bezier.Curve(nodes1, degree=2)
>>> nodes2 = np.asfortranarray([
... [ 1.5625, -1.5625, 1.5625],
... [-0.0625, 0.25 , 0.5625],
... ])
>>> curve2 = bezier.Curve(nodes2, degree=2)
>>> intersections = curve1.intersect(curve2)
>>> sq5 = np.sqrt(5.0)
>>> expected_ints = np.asfortranarray([
... [4 - sq5, 3, 9, 4 + sq5],
... [6 - sq5, 7, 1, 6 + sq5],
... ]) / 10.0
>>> max_err = np.max(np.abs(intersections - expected_ints))
>>> binary_exponent(max_err) <= -51
True
>>> s_vals = np.asfortranarray(intersections[0, :])
>>> points = curve1.evaluate_multi(s_vals)
>>> expected_pts = np.asfortranarray([
... [6 - 2 * sq5, 4, 16, 6 + 2 * sq5],
... [ 5 - sq5, 6, 0, 5 + sq5 ],
... ]) / 16.0
>>> max_err = np.max(np.abs(points - expected_pts))
>>> binary_exponent(max_err)
-53
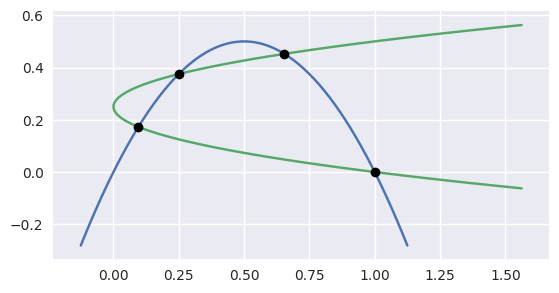
For higher degree intersections, the error starts to get a little larger.
>>> nodes1 = np.asfortranarray([
... [0.25 , 0.625, 1.0],
... [0.625, 0.25 , 1.0],
... ])
>>> curve1 = bezier.Curve(nodes1, degree=2)
>>> nodes2 = np.asfortranarray([
... [0.0, 0.25, 0.75, 1.0],
... [0.5, 1.0 , 1.5 , 0.5],
... ])
>>> curve2 = bezier.Curve(nodes2, degree=3)
>>> intersections = curve1.intersect(curve2)
>>> s_vals = np.roots([486, -3726, 13905, -18405, 6213, 1231])
>>> _, s_val, _ = np.sort(s_vals[s_vals.imag == 0].real)
>>> t_vals = np.roots([4, -16, 13, 25, -28, 4])
>>> _, _, t_val = np.sort(t_vals[t_vals.imag == 0].real)
>>> expected_ints = np.asfortranarray([
... [s_val],
... [t_val],
... ])
>>> max_err = np.max(np.abs(intersections - expected_ints))
>>> binary_exponent(max_err)
-50
>>> s_vals = np.asfortranarray(intersections[0, :])
>>> points = curve1.evaluate_multi(s_vals)
>>> x_val = (3 * s_val + 1) / 4
>>> y_val = (9 * s_val * s_val - 6 * s_val + 5) / 8
>>> expected_pts = np.asfortranarray([
... [x_val],
... [y_val],
... ])
>>> max_err = np.max(np.abs(points - expected_pts))
>>> binary_exponent(max_err) <= -50
True
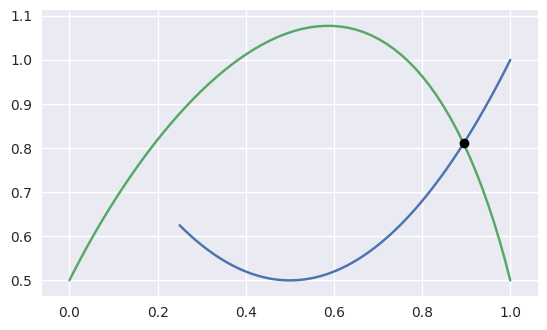
>>> nodes1 = np.asfortranarray([
... [0.0, 6.0],
... [8.0, 0.0],
... ])
>>> curve1 = bezier.Curve(nodes1, degree=1)
>>> nodes2 = np.asfortranarray([
... [0.375, 2.125, 3.875, 5.625],
... [7.0 , 8.0 , 0.0 , 1.0 ],
... ])
>>> curve2 = bezier.Curve(nodes2, degree=3)
>>> intersections = curve1.intersect(curve2)
>>> sq7 = np.sqrt(7.0)
>>> expected_ints = np.asfortranarray([
... [24, 24 - 7 * sq7, 24 + 7 * sq7],
... [24, 24 - 8 * sq7, 24 + 8 * sq7],
... ]) / 48.0
>>> max_err = np.max(np.abs(intersections - expected_ints))
>>> binary_exponent(max_err)
-52
>>> s_vals = np.asfortranarray(intersections[0, :])
>>> points = curve1.evaluate_multi(s_vals)
>>> expected_pts = np.asfortranarray([
... [72, 72 - 21 * sq7, 72 + 21 * sq7],
... [96, 96 + 28 * sq7, 96 - 28 * sq7],
... ]) / 24.0
>>> max_err = np.max(np.abs(points - expected_pts))
>>> binary_exponent(max_err)
-50
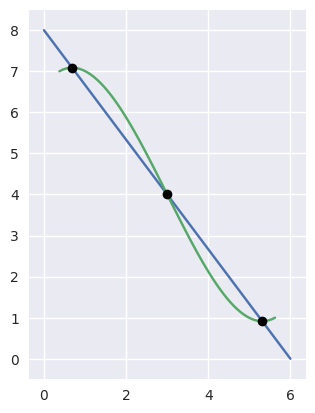
>>> nodes1 = np.asfortranarray([
... [0.0 , 1.0 ],
... [0.375, 0.375],
... ])
>>> curve1 = bezier.Curve(nodes1, degree=1)
>>> nodes2 = np.asfortranarray([
... [0.125, 0.375, 0.625, 0.875 ],
... [0.25 , 0.75 , 0.0 , 0.1875],
... ])
>>> curve2 = bezier.Curve(nodes2, degree=3)
>>> intersections = curve1.intersect(curve2)
>>> s_vals = np.asfortranarray(intersections[0, :])
>>> points = curve1.evaluate_multi(s_vals)
>>> s_val2, s_val1, _ = np.sort(np.roots(
... [17920, -29760, 13512, -1691]))
>>> t_val2, t_val1, _ = np.sort(np.roots([35, -60, 24, -2]))
>>> expected_ints = np.asfortranarray([
... [s_val1, s_val2],
... [t_val1, t_val2],
... ])
>>> max_err = np.max(np.abs(intersections - expected_ints))
>>> binary_exponent(max_err) <= -51
True
>>> expected_pts = np.asfortranarray([
... [s_val1, s_val2],
... [ 0.375, 0.375 ],
... ])
>>> max_err = np.max(np.abs(points - expected_pts))
>>> binary_exponent(max_err) <= -51
True
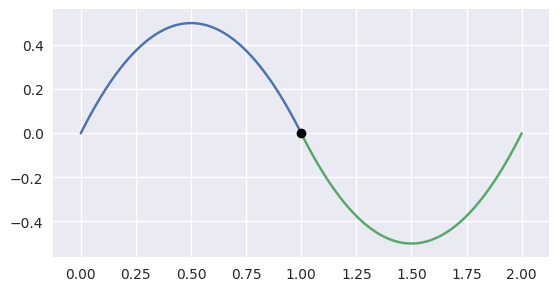
Intersections at Endpoints¶
>>> nodes1 = np.asfortranarray([
... [0.0, 0.5, 1.0],
... [0.0, 1.0, 0.0],
... ])
>>> curve1 = bezier.Curve(nodes1, degree=2)
>>> nodes2 = np.asfortranarray([
... [1.0, 1.5, 2.0],
... [0.0, -1.0, 0.0],
... ])
>>> curve2 = bezier.Curve(nodes2, degree=2)
>>> intersections = curve1.intersect(curve2)
>>> intersections
array([[1.],
[0.]])
>>> s_vals = np.asfortranarray(intersections[0, :])
>>> curve1.evaluate_multi(s_vals)
array([[1.],
[0.]])
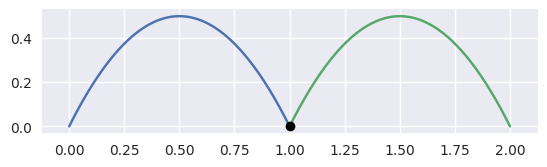
>>> nodes1 = np.asfortranarray([
... [0.0, 0.5, 1.0],
... [0.0, 1.0, 0.0],
... ])
>>> curve1 = bezier.Curve(nodes1, degree=2)
>>> nodes2 = np.asfortranarray([
... [2.0, 1.5, 1.0],
... [0.0, 1.0, 0.0],
... ])
>>> curve2 = bezier.Curve(nodes2, degree=2)
>>> intersections = curve1.intersect(curve2)
>>> intersections
array([[1.],
[1.]])
>>> s_vals = np.asfortranarray(intersections[0, :])
>>> curve1.evaluate_multi(s_vals)
array([[1.],
[0.]])
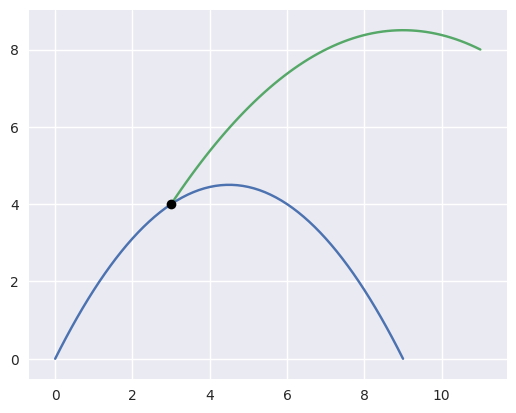
>>> nodes1 = np.asfortranarray([
... [0.0, 4.5, 9.0],
... [0.0, 9.0, 0.0],
... ])
>>> curve1 = bezier.Curve(nodes1, degree=2)
>>> nodes2 = np.asfortranarray([
... [11.0, 7.0, 3.0],
... [ 8.0, 10.0, 4.0],
... ])
>>> curve2 = bezier.Curve(nodes2, degree=2)
>>> intersections = curve1.intersect(curve2)
>>> intersections
array([[0.333...],
[1. ]])
>>> s_vals = np.asfortranarray(intersections[0, :])
>>> curve1.evaluate_multi(s_vals)
array([[3.],
[4.]])
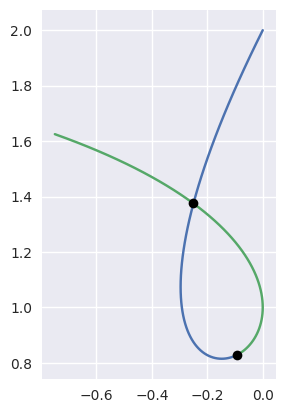
Detecting Self-Intersections¶
>>> nodes = np.asfortranarray([
... [0.0, -1.0, 1.0, -0.75 ],
... [2.0, 0.0, 1.0, 1.625],
... ])
>>> curve = bezier.Curve(nodes, degree=3)
>>> left, right = curve.subdivide()
>>> intersections = left.intersect(right)
>>> sq5 = np.sqrt(5.0)
>>> expected_ints = np.asfortranarray([
... [3, 3 - sq5],
... [0, sq5 ],
... ]) / 3.0
>>> max_err = np.max(np.abs(intersections - expected_ints))
>>> binary_exponent(max_err)
-53
>>> s_vals = np.asfortranarray(intersections[0, :])
>>> left.evaluate_multi(s_vals)
array([[-0.09375 , -0.25 ],
[ 0.828125, 1.375 ]])
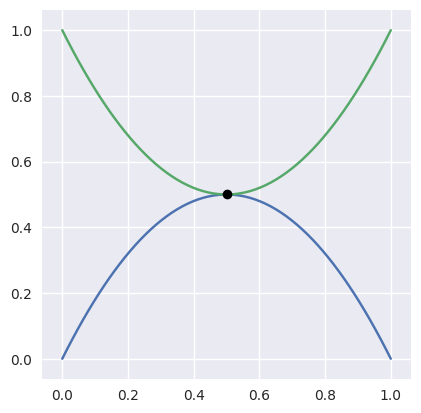
Limitations¶
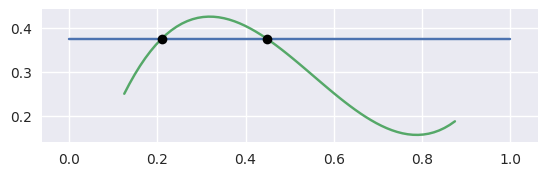
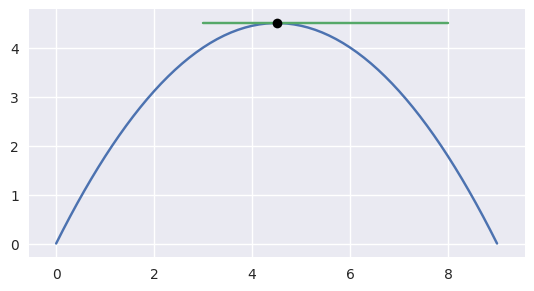
Intersections that occur at points of tangency are in general problematic. For example, consider
The first curve is the zero set of \(y - 2x(1 - x)\), so plugging in the second curve gives
This shows that a point of tangency is equivalent to a repeated root of a polynomial. For this example, the intersection process successfully terminates
>>> nodes1 = np.asfortranarray([
... [0.0, 0.5, 1.0],
... [0.0, 1.0, 0.0],
... ])
>>> curve1 = bezier.Curve(nodes1, degree=2)
>>> nodes2 = np.asfortranarray([
... [0.0, 0.5, 1.0],
... [1.0, 0.0, 1.0],
... ])
>>> curve2 = bezier.Curve(nodes2, degree=2)
>>> intersections = curve1.intersect(curve2)
>>> intersections
array([[0.5],
[0.5]])
>>> s_vals = np.asfortranarray(intersections[0, :])
>>> curve1.evaluate_multi(s_vals)
array([[0.5],
[0.5]])
This library makes an earnest effort to compute tangent intersections. For example, when the curves
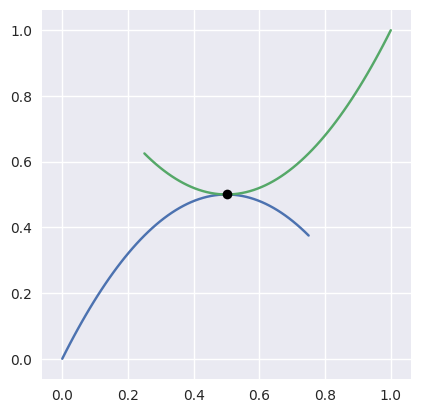
have been subdivided and approximated by lines, the corresponding segments are parallel, hence don’t intersect. At this point, this library detects the problematic intersection point and switches to a more robust Newton’s method that is built to handle the numerical issue caused by the double root.
Unlike the first tangent example, this intersection occurs at parameters which are not exact floating point numbers:
>>> nodes1 = np.asfortranarray([
... [0.0, 0.375, 0.75 ],
... [0.0, 0.75 , 0.375],
... ])
>>> curve1 = bezier.Curve(nodes1, degree=2)
>>> nodes2 = np.asfortranarray([
... [0.25 , 0.625, 1.0],
... [0.625, 0.25 , 1.0],
... ])
>>> curve2 = bezier.Curve(nodes2, degree=2)
>>> intersections = curve1.intersect(curve2)
>>> intersections
array([[0.6666...],
[0.3333...]])
>>> s_vals = np.asfortranarray(intersections[0, :])
>>> curve1.evaluate_multi(s_vals)
array([[0.5],
[0.5]])
See another case where one parameter is an exact floating point number and the other is not:
>>> nodes1 = np.asfortranarray([
... [0.0, 4.5, 9.0],
... [0.0, 9.0, 0.0],
... ])
>>> curve1 = bezier.Curve(nodes1, degree=2)
>>> nodes2 = np.asfortranarray([
... [3.0, 8.0],
... [4.5, 4.5],
... ])
>>> curve2 = bezier.Curve(nodes2, degree=1)
>>> intersections = curve1.intersect(curve2)
>>> intersections
array([[0.5],
[0.3]])
>>> s_vals = np.asfortranarray(intersections[0, :])
>>> curve1.evaluate_multi(s_vals)
array([[4.5],
[4.5]])
In addition to points of tangency, coincident curve segments are partially supported (but are in general hard to detect). For the curves
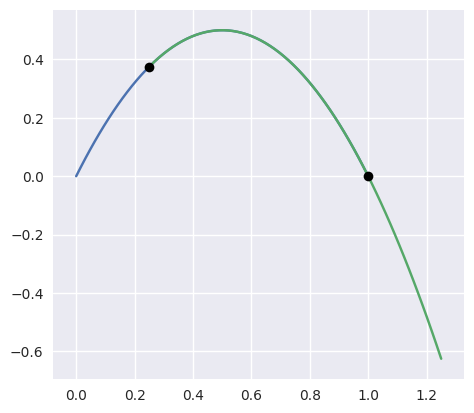
the library determines the “intersection” points as the beginning and end of the segment that is common to both curves:
>>> nodes1 = np.asfortranarray([
... [0.0, 0.5, 1.0],
... [0.0, 1.0, 0.0],
... ])
>>> curve1 = bezier.Curve(nodes1, degree=2)
>>> nodes2 = np.asfortranarray([
... [0.25, 0.75, 1.25],
... [0.375, 0.875, -0.625],
... ])
>>> curve2 = bezier.Curve(nodes2, degree=2)
>>> curve1.intersect(curve2)
array([[0.25, 1. ],
[0. , 0.75]])