bezier¶
Helper for Bézier Curves, Triangles, and Higher Order Objects
This library provides:
Dive in and take a look!
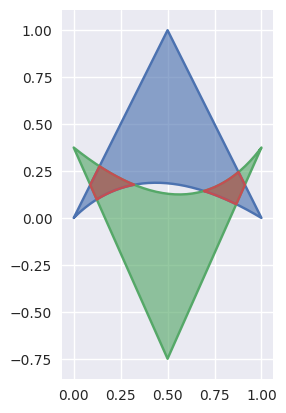
Why Bézier?¶
A Bézier curve (and triangle, etc.) is a parametric curve that uses the Bernstein basis:
to define a curve as a linear combination:
This comes from the fact that the weights sum to one:
This can be generalized to higher order by considering three, four, etc. non-negative weights that sum to one (in the above we have the two non-negative weights \(s\) and \(1 - s\)).
Due to their simple form, Bézier curves:
can easily model geometric objects as parametric curves, triangles, etc.
can be computed in an efficient and numerically stable way via de Casteljau’s algorithm
can utilize convex optimization techniques for many algorithms (such as curve-curve intersection), since curves (and triangles, etc.) are convex combinations of the basis
Many applications – as well as the history of their development – are described in “The Bernstein polynomial basis: A centennial retrospective”, for example;
Installing¶
The bezier Python package can be installed with pip:
$ python -m pip install --upgrade bezier
$ python3.8 -m pip install --upgrade bezier
$ # To install optional dependencies, e.g. SymPy
$ python -m pip install --upgrade bezier[full]
To install a pure Python version (i.e. with no binary extension):
$ BEZIER_NO_EXTENSION=true \
> python -m pip install --upgrade bezier --no-binary=bezier
bezier is open-source, so you can alternatively grab the source
code from GitHub and install from source.
Getting Started¶
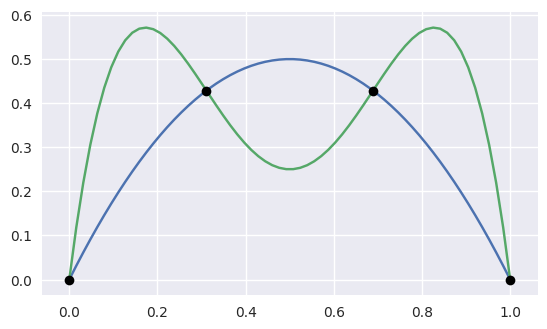
For example, to create a curve:
>>> nodes1 = np.asfortranarray([
... [0.0, 0.5, 1.0],
... [0.0, 1.0, 0.0],
... ])
>>> curve1 = bezier.Curve(nodes1, degree=2)
The intersection (points) between two curves can also be determined:
>>> nodes2 = np.asfortranarray([
... [0.0, 0.25, 0.5, 0.75, 1.0],
... [0.0, 2.0 , -2.0, 2.0 , 0.0],
... ])
>>> curve2 = bezier.Curve.from_nodes(nodes2)
>>> intersections = curve1.intersect(curve2)
>>> intersections
array([[0.31101776, 0.68898224, 0. , 1. ],
[0.31101776, 0.68898224, 0. , 1. ]])
>>> s_vals = np.asfortranarray(intersections[0, :])
>>> points = curve1.evaluate_multi(s_vals)
>>> points
array([[0.31101776, 0.68898224, 0. , 1. ],
[0.42857143, 0.42857143, 0. , 0. ]])
and then we can plot these curves (along with their intersections):
>>> import matplotlib.pyplot as plt
>>> import seaborn
>>> seaborn.set()
>>>
>>> ax = curve1.plot(num_pts=256)
>>> _ = curve2.plot(num_pts=256, ax=ax)
>>> lines = ax.plot(
... points[0, :], points[1, :],
... marker="o", linestyle="None", color="black")
>>> _ = ax.axis("scaled")
>>> _ = ax.set_xlim(-0.125, 1.125)
>>> _ = ax.set_ylim(-0.0625, 0.625)
>>> plt.show()
For API-level documentation, check out the Bézier Python package documentation.
Development¶
To work on adding a feature or to run the functional tests, see the DEVELOPMENT doc for more information on how to get started.
Citation¶
For publications that use bezier, there is a JOSS paper that can be
cited. The following BibTeX entry can be used:
@article{Hermes2017,
doi = {10.21105/joss.00267},
url = {https://doi.org/10.21105%2Fjoss.00267},
year = {2017},
month = {Aug},
publisher = {The Open Journal},
volume = {2},
number = {16},
pages = {267},
author = {Danny Hermes},
title = {Helper for B{\'{e}}zier Curves, Triangles, and Higher Order Objects},
journal = {The Journal of Open Source Software}
}
A particular version of this library can be cited via a Zenodo DOI; see a full list by version.
License¶
bezier is made available under the Apache 2.0 License. For more
details, see the LICENSE.
