bezier.curve module¶
Helper for Bézier Curves.
See Curve-Curve Intersection for examples using the
Curve class to find intersections.
-
class
bezier.curve.Curve(nodes, start=0.0, end=1.0, root=None, _copy=True)¶ Bases:
bezier._base.BaseRepresents a Bézier curve.
We take the traditional definition: a Bézier curve is a mapping from \(s \in \left[0, 1\right]\) to convex combinations of points \(v_0, v_1, \ldots, v_n\) in some vector space:
\[B(s) = \sum_{j = 0}^n \binom{n}{j} s^j (1 - s)^{n - j} \cdot v_j\]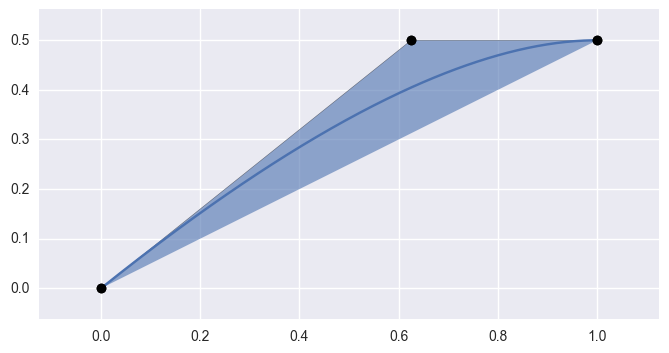
>>> import bezier >>> nodes = np.array([ ... [0.0 , 0.0], ... [0.625, 0.5], ... [1.0 , 0.5], ... ]) >>> curve = bezier.Curve(nodes) >>> curve <Curve (degree=2, dimension=2)>
Parameters: - nodes (numpy.ndarray) – The nodes in the curve. The rows represent each node while the columns are the dimension of the ambient space.
- start (
Optional[float]) – The beginning of the sub-interval that this curve represents. - end (
Optional[float]) – The end of the sub-interval that this curve represents. - root (
Optional[Curve]) – The root curve that contains this current curve. - _copy (bool) – Flag indicating if the nodes should be copied before
being stored. Defaults to
Truesince callers may freely mutatenodesafter passing in.
-
length¶ float: The length of the current curve.
-
start¶ float: Start of sub-interval this curve represents.
This value is used to track the current curve in the re-parameterization / subdivision process. The curve is still defined on the unit interval, but this value illustrates how this curve relates to a “parent” curve. For example:
>>> nodes = np.array([ ... [0.0, 0.0], ... [1.0, 2.0], ... ]) >>> curve = bezier.Curve(nodes) >>> curve <Curve (degree=1, dimension=2)> >>> left, right = curve.subdivide() >>> left <Curve (degree=1, dimension=2, start=0, end=0.5)> >>> right <Curve (degree=1, dimension=2, start=0.5, end=1)> >>> _, mid_right = left.subdivide() >>> mid_right <Curve (degree=1, dimension=2, start=0.25, end=0.5)> >>> mid_right.nodes array([[ 0.25, 0.5 ], [ 0.5 , 1. ]])
-
root¶ Curve: The “root” curve that contains the current curve.
This indicates that the current curve is a section of the “root” curve. For example:
>>> _, right = curve.subdivide() >>> right <Curve (degree=2, dimension=2, start=0.5, end=1)> >>> right.root is curve True >>> right.evaluate(0.0) == curve.evaluate(0.5) array([ True, True], dtype=bool) >>> >>> mid_left, _ = right.subdivide() >>> mid_left <Curve (degree=2, dimension=2, start=0.5, end=0.75)> >>> mid_left.root is curve True >>> mid_left.evaluate(1.0) == curve.evaluate(0.75) array([ True, True], dtype=bool)
-
edge_index¶ Optional[int] : The index of the edge among a group of edges.>>> curve.edge_index 1 >>> curve.previous_edge <Curve (degree=1, dimension=2)> >>> curve.previous_edge.edge_index 0 >>> curve.next_edge <Curve (degree=1, dimension=2)> >>> curve.next_edge.edge_index 2
This is intended to be used when a
Curveis created as part of a larger structure like aSurfaceorCurvedPolygon.
-
next_edge¶ Optional[Curve] : An edge that comes after the current one.This is intended to be used when a
Curveis created as part of a larger structure like aSurfaceorCurvedPolygon.
-
previous_edge¶ Optional[Curve] : An edge that comes before the current one.This is intended to be used when a
Curveis created as part of a larger structure like aSurfaceorCurvedPolygon.
-
evaluate(s)¶ Evaluate \(B(s)\) along the curve.
See
evaluate_multi()for more details.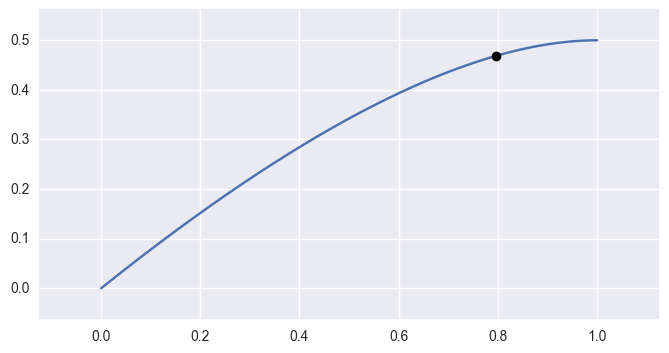
>>> nodes = np.array([ ... [0.0 , 0.0], ... [0.625, 0.5], ... [1.0 , 0.5], ... ]) >>> curve = bezier.Curve(nodes) >>> curve.evaluate(0.75) array([ 0.796875, 0.46875 ])
Parameters: s (float) – Parameter along the curve. Returns: The point on the curve (as a one dimensional NumPy array). Return type: numpy.ndarray
-
evaluate_multi(s_vals)¶ Evaluate \(B(s)\) for multiple points along the curve.
This is done by first evaluating each member of the Bernstein basis at each value in
s_valsand then applying those to the control points for the current curve.This is done instead of using de Casteljau’s algorithm. Implementing de Casteljau is problematic because it requires a choice between one of two methods:
- vectorize operations of the form \((1 - s)v + s w\),
which requires a copy of the curve’s control points for
each value in
s_vals - avoid vectorization and compute each point in serial
Instead, we can use vectorized operations to build up the Bernstein basis values.
>>> nodes = np.array([ ... [0.0, 0.0, 0.0], ... [1.0, 2.0, 3.0], ... ]) >>> curve = bezier.Curve(nodes) >>> curve <Curve (degree=1, dimension=3)> >>> s_vals = np.linspace(0.0, 1.0, 5) >>> curve.evaluate_multi(s_vals) array([[ 0. , 0. , 0. ], [ 0.25, 0.5 , 0.75], [ 0.5 , 1. , 1.5 ], [ 0.75, 1.5 , 2.25], [ 1. , 2. , 3. ]])
Parameters: s_vals (numpy.ndarray) – Parameters along the curve (as a 1D array). Returns: The points on the curve. As a two dimensional NumPy array, with the rows corresponding to each svalue and the columns to the dimension.Return type: numpy.ndarray - vectorize operations of the form \((1 - s)v + s w\),
which requires a copy of the curve’s control points for
each value in
-
plot(num_pts, ax=None, show=False)¶ Plot the current curve.
Parameters: - num_pts (int) – Number of points to plot.
- ax (
Optional[matplotlib.artist.Artist]) – matplotlib axis object to add plot to. - show (
Optional[bool]) – Flag indicating if the plot should be shown.
Returns: The axis containing the plot. This may be a newly created axis.
Return type: Raises: NotImplementedError– If the curve’s dimension is not2.
-
subdivide()¶ Split the curve \(B(s)\) into a left and right half.
Takes the interval \(\left[0, 1\right]\) and splits the curve into \(B_1 = B\left(\left[0, \frac{1}{2}\right]\right)\) and \(B_2 = B\left(\left[\frac{1}{2}, 1\right]\right)\). In order to do this, also reparameterizes the curve, hence the resulting left and right halves have new nodes.
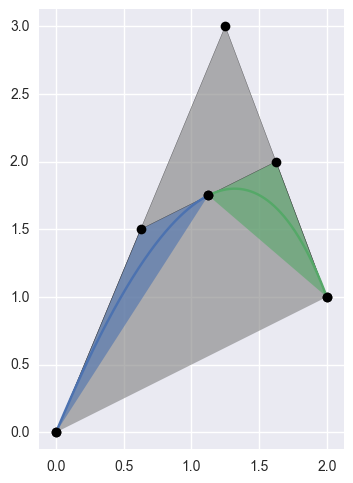
>>> nodes = np.array([ ... [0.0 , 0.0], ... [1.25, 3.0], ... [2.0 , 1.0], ... ]) >>> curve = bezier.Curve(nodes) >>> left, right = curve.subdivide() >>> left <Curve (degree=2, dimension=2, start=0, end=0.5)> >>> left.nodes array([[ 0. , 0. ], [ 0.625, 1.5 ], [ 1.125, 1.75 ]]) >>> right <Curve (degree=2, dimension=2, start=0.5, end=1)> >>> right.nodes array([[ 1.125, 1.75 ], [ 1.625, 2. ], [ 2. , 1. ]])
Returns: The left and right sub-curves. Return type: Tuple[Curve,Curve]
-
intersect(other)¶ Find the points of intersection with another curve.
See Curve-Curve Intersection for more details.
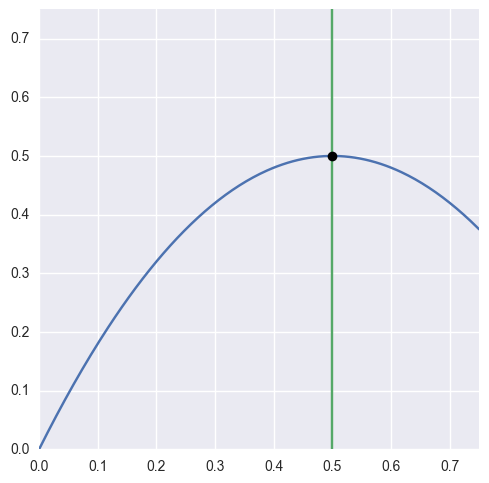
>>> nodes1 = np.array([ ... [0.0 , 0.0 ], ... [0.375, 0.75 ], ... [0.75 , 0.375], ... ]) >>> curve1 = bezier.Curve(nodes1) >>> nodes2 = np.array([ ... [0.5, 0.0 ], ... [0.5, 0.75], ... ]) >>> curve2 = bezier.Curve(nodes2) >>> intersections = curve1.intersect(curve2) >>> intersections array([[ 0.5, 0.5]])
Parameters: other (Curve) – Other curve to intersect with.
Returns: Array of intersection points (possibly empty).
Return type: Raises: TypeError– Ifotheris not a curve.NotImplementedError– If both curves aren’t two-dimensional.
-
elevate()¶ Return a degree-elevated version of the current curve.
Does this by converting the current nodes \(v_0, \ldots, v_n\) to new nodes \(w_0, \ldots, w_{n + 1}\) where
\[\begin{split}\begin{align*} w_0 &= v_0 \\ w_j &= \frac{j}{n + 1} v_{j - 1} + \frac{n + 1 - j}{n + 1} v_j \\ w_{n + 1} &= v_n \end{align*}\end{split}\]Returns: The degree-elevated curve. Return type: Curve
-
__eq__(other)¶ Check equality against another shape.
Returns: Boolean indicating if the shapes are the same. Return type: bool
-
__ne__(other)¶ Check inequality against another shape.
Returns: Boolean indicating if the shapes are not the same. Return type: bool
-
copy()¶ Make a copy of the current shape.
Returns: Instance of the current shape.
-
degree¶ int: The degree of the current shape.
-
dimension¶ int: The dimension that the shape lives in.
For example, if the shape lives in \(\mathbf{R}^3\), then the dimension is
3.
-
nodes¶ numpy.ndarray: The nodes that define the current shape.
-
specialize(start, end)¶ Specialize the curve to a given sub-interval.
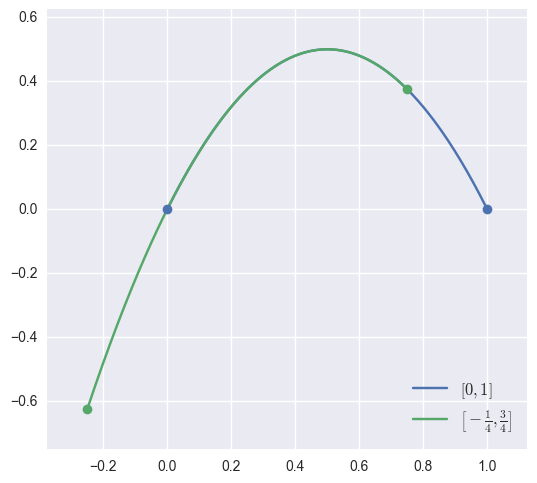
>>> curve = bezier.Curve(np.array([ ... [0.0, 0.0], ... [0.5, 1.0], ... [1.0, 0.0], ... ])) >>> new_curve = curve.specialize(-0.25, 0.75) >>> new_curve <Curve (degree=2, dimension=2, start=-0.25, end=0.75)> >>> new_curve.nodes array([[-0.25 , -0.625], [ 0.25 , 0.875], [ 0.75 , 0.375]])
This is generalized version of
subdivide(), and can even match the output of that method:>>> left, right = curve.subdivide() >>> left == curve.specialize(0.0, 0.5) True >>> right == curve.specialize(0.5, 1.0) True
Parameters: Returns: The newly-specialized curve.
Return type: