Algorithm Helpers¶
In an attempt to thoroughly vet each algorithm used in this library, each computation is split into small units that can be tested independently.
Though many of these computational units aren’t provided as part of the public interface of this library, they are still interesting. (Possibly) more importantly, it’s useful to see these algorithms at work.
In this document, these helper functions and objects are documented. This is to help with the exposition of the computation and does not imply that these are part of the stable public interface.
-
bezier._intersection_helpers.linearization_error(curve)¶ Compute the maximum error of a linear approximation.
Helper for
Linearization, which is used during the curve-curve intersection process.We use the line
\[L(s) = v_0 (1 - s) + v_n s\]and compute a bound on the maximum error
\[\max_{s \in \left[0, 1\right]} \|B(s) - L(s)\|_2.\]Rather than computing the actual maximum (a tight bound), we use an upper bound via the remainder from Lagrange interpolation in each component. This leaves us with \(\frac{s(s - 1)}{2!}\) times the second derivative in each component.
The second derivative curve is degree \(d = n - 2\) and is given by
\[B''(s) = n(n - 1) \sum_{j = 0}^{d} \binom{d}{j} s^j (1 - s)^{d - j} \cdot \Delta^2 v_j\]Due to this form (and the convex combination property of Bézier Curves) we know each component of the second derivative will be bounded by the maximum of that component among the \(\Delta^2 v_j\).
For example, the curve
\[\begin{split}B(s) = \left[\begin{array}{c} 0 \\ 0 \end{array}\right] (1 - s)^2 + \left[\begin{array}{c} 3 \\ 1 \end{array}\right] 2s(1 - s) + \left[\begin{array}{c} 9 \\ -2 \end{array}\right] s^2\end{split}\]has \(B''(s) \equiv \left[\begin{array}{c} 6 \\ -8 \end{array}\right]\) which has norm \(10\) everywhere, hence the maximum error is
\[\left.\frac{s(1 - s)}{2!} \cdot 10\right|_{s = \frac{1}{2}} = \frac{5}{4}.\]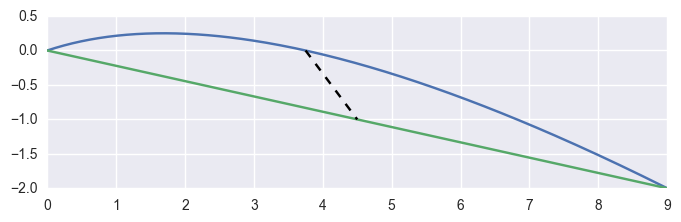
>>> nodes = np.array([ ... [0.0, 0.0], ... [3.0, 1.0], ... [9.0, -2.0], ... ]) >>> curve = bezier.Curve(nodes) >>> linearization_error(curve) 1.25
As a non-example, consider a “pathological” set of control points:
\[\begin{split}B(s) = \left[\begin{array}{c} 0 \\ 0 \end{array}\right] (1 - s)^3 + \left[\begin{array}{c} 5 \\ 12 \end{array}\right] 3s(1 - s)^2 + \left[\begin{array}{c} 10 \\ 24 \end{array}\right] 3s^2(1 - s) + \left[\begin{array}{c} 30 \\ 72 \end{array}\right] s^3\end{split}\]By construction, this lies on the line \(y = \frac{12x}{5}\), but the parametrization is cubic: \(12 \cdot x(s) = 5 \cdot y(s) = 180s(s^2 + 1)\). Hence, the fact that the curve is a line is not accounted for and we take the worse case among the nodes in:
\[\begin{split}B''(s) = 3 \cdot 2 \cdot \left( \left[\begin{array}{c} 0 \\ 0 \end{array}\right] (1 - s) + \left[\begin{array}{c} 15 \\ 36 \end{array}\right] s\right)\end{split}\]which gives a nonzero maximum error:
>>> nodes = np.array([ ... [ 0.0, 0.0], ... [ 5.0, 12.0], ... [10.0, 24.0], ... [30.0, 72.0], ... ]) >>> curve = bezier.Curve(nodes) >>> linearization_error(curve) 29.25
Though it may seem that
0is a more appropriate answer, consider the goal of this function. We seek to linearize curves and then intersect the linear approximations. Then the \(s\)-values from the line-line intersection is lifted back to the curves. Thus the error \(\|B(s) - L(s)\|_2\) is more relevant than the underyling algebraic curve containing \(B(s)\).Note
It may be more appropriate to use a relative linearization error rather than the absolute error provided here. It’s unclear if the domain \(\left[0, 1\right]\) means the error is already adequately scaled or if the error should be scaled by the arc length of the curve or the (easier-to-compute) length of the line.
Parameters: curve (Curve) – A curve to be approximated by a line. Returns: The maximum error between the curve and the linear approximation. Return type: float
-
bezier._intersection_helpers.newton_refine(s, curve1, t, curve2)¶ Apply one step of 2D Newton’s method.
We want to use Newton’s method on the function
\[F(s, t) = B_1(s) - B_2(t)\]to refine \(\left(s_{\ast}, t_{\ast}\right)\). Using this, and the Jacobian \(DF\), we “solve”
\[\begin{split}\left[\begin{array}{c} 0 \\ 0 \end{array}\right] \approx F\left(s_{\ast} + \Delta s, t_{\ast} + \Delta t\right) \approx F\left(s_{\ast}, t_{\ast}\right) + \left[\begin{array}{c c} B_1'\left(s_{\ast}\right) & - B_2'\left(t_{\ast}\right) \end{array}\right] \left[\begin{array}{c} \Delta s \\ \Delta t \end{array}\right]\end{split}\]and refine with the component updates \(\Delta s\) and \(\Delta t\).
Note
This implementation assumes
curve1andcurve2live in \(\mathbf{R}^2\).For example, the curves
\[\begin{split}\begin{align*} B_1(s) &= \left[\begin{array}{c} 0 \\ 0 \end{array}\right] (1 - s)^2 + \left[\begin{array}{c} 2 \\ 4 \end{array}\right] 2s(1 - s) + \left[\begin{array}{c} 4 \\ 0 \end{array}\right] s^2 \\ B_2(t) &= \left[\begin{array}{c} 2 \\ 0 \end{array}\right] (1 - t) + \left[\begin{array}{c} 0 \\ 3 \end{array}\right] t \end{align*}\end{split}\]intersect at the point \(B_1\left(\frac{1}{4}\right) = B_2\left(\frac{1}{2}\right) = \frac{1}{2} \left[\begin{array}{c} 2 \\ 3 \end{array}\right]\).
However, starting from the wrong point we have
\[\begin{split}\begin{align*} F\left(\frac{3}{8}, \frac{1}{4}\right) &= \frac{1}{8} \left[\begin{array}{c} 0 \\ 9 \end{array}\right] \\ DF\left(\frac{3}{8}, \frac{1}{4}\right) &= \left[\begin{array}{c c} 4 & 2 \\ 2 & -3 \end{array}\right] \\ \Longrightarrow \left[\begin{array}{c} \Delta s \\ \Delta t \end{array}\right] &= \frac{9}{64} \left[\begin{array}{c} -1 \\ 2 \end{array}\right]. \end{align*}\end{split}\]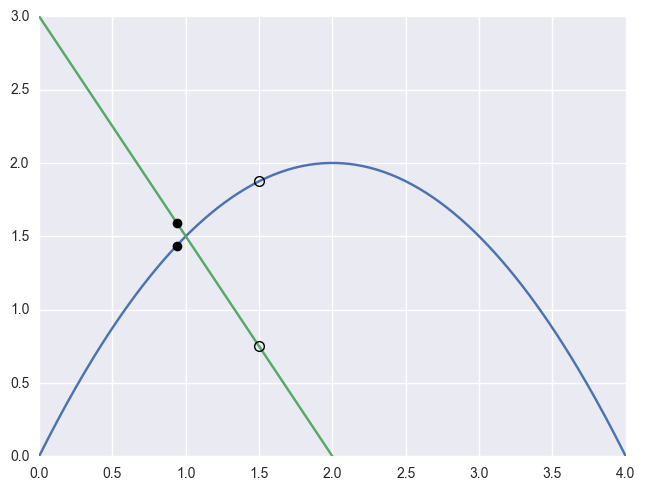
>>> nodes1 = np.array([ ... [0.0, 0.0], ... [2.0, 4.0], ... [4.0, 0.0], ... ]) >>> curve1 = bezier.Curve(nodes1) >>> nodes2 = np.array([ ... [2.0, 0.0], ... [0.0, 3.0], ... ]) >>> curve2 = bezier.Curve(nodes2) >>> s, t = 0.375, 0.25 >>> new_s, new_t = newton_refine(s, curve1, t, curve2) >>> 64.0 * (new_s - s) -9.0 >>> 64.0 * (new_t - t) 18.0
For “typical” curves, we converge to a solution quadratically. This means that the number of correct digits doubles every iteration (until machine precision is reached).
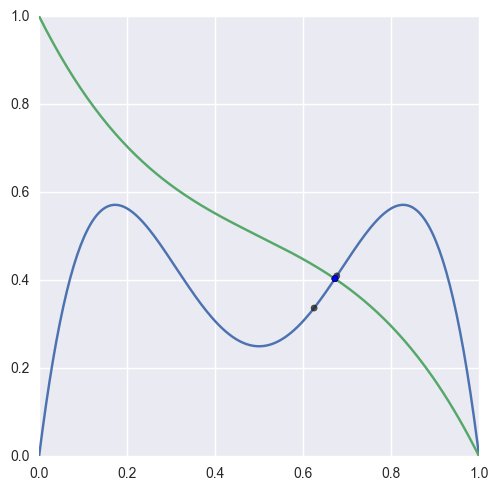
>>> curve1 = bezier.Curve(np.array([ ... [0.0, 0.0], ... [0.25, 2.0], ... [0.5, -2.0], ... [0.75, 2.0], ... [1.0, 0.0], ... ])) >>> curve2 = bezier.Curve(np.array([ ... [0.0, 1.0], ... [0.25, 0.5], ... [0.5, 0.5], ... [0.75, 0.5], ... [1.0, 0.0], ... ])) >>> # The expected intersection is the only real root of >>> # 28 s^3 - 30 s^2 + 9 s - 1. >>> omega = (28.0 * np.sqrt(17.0) + 132.0)**(1.0 / 3.0) / 28.0 >>> expected = 5.0 / 14.0 + omega + 1 / (49.0 * omega) >>> s_vals = [0.625, None, None, None, None] >>> t = 0.625 >>> np.log2(abs(expected - s_vals[0])) -4.399... >>> s_vals[1], t = newton_refine(s_vals[0], curve1, t, curve2) >>> np.log2(abs(expected - s_vals[1])) -7.901... >>> s_vals[2], t = newton_refine(s_vals[1], curve1, t, curve2) >>> np.log2(abs(expected - s_vals[2])) -16.010... >>> s_vals[3], t = newton_refine(s_vals[2], curve1, t, curve2) >>> np.log2(abs(expected - s_vals[3])) -32.110... >>> s_vals[4], t = newton_refine(s_vals[3], curve1, t, curve2) >>> s_vals[4] == expected True
However, when the intersection occurs at a point of tangency, the convergence becomes linear. This means that the number of correct digits added each iteration is roughly constant.
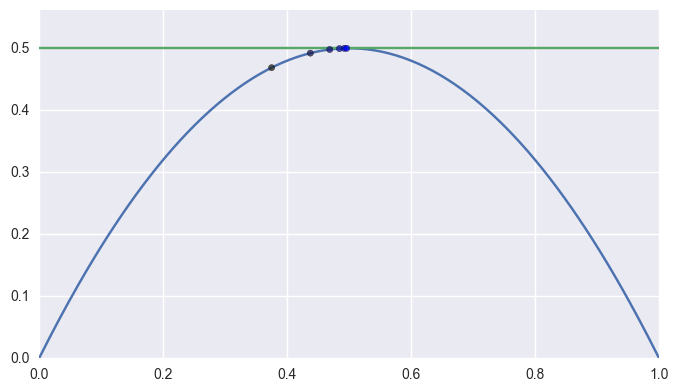
>>> curve1 = bezier.Curve(np.array([ ... [0.0, 0.0], ... [0.5, 1.0], ... [1.0, 0.0], ... ])) >>> curve2 = bezier.Curve(np.array([ ... [0.0, 0.5], ... [1.0, 0.5], ... ])) >>> expected = 0.5 >>> s_vals = [0.375, None, None, None, None, None] >>> t = 0.375 >>> np.log2(abs(expected - s_vals[0])) -3.0 >>> s_vals[1], t = newton_refine(s_vals[0], curve1, t, curve2) >>> np.log2(abs(expected - s_vals[1])) -4.0 >>> s_vals[2], t = newton_refine(s_vals[1], curve1, t, curve2) >>> np.log2(abs(expected - s_vals[2])) -5.0 >>> s_vals[3], t = newton_refine(s_vals[2], curve1, t, curve2) >>> np.log2(abs(expected - s_vals[3])) -6.0 >>> s_vals[4], t = newton_refine(s_vals[3], curve1, t, curve2) >>> np.log2(abs(expected - s_vals[4])) -7.0 >>> s_vals[5], t = newton_refine(s_vals[4], curve1, t, curve2) >>> np.log2(abs(expected - s_vals[5])) -8.0
Unfortunately, the process terminates with an error that is not close to machine precision \(\varepsilon\) when \(\Delta s = \Delta t = 0\).
>>> s1 = t1 = 0.5 - 0.5**27 >>> np.log2(0.5 - s1) -27.0 >>> s2, t2 = newton_refine(s1, curve1, t1, curve2) >>> s2 == t2 True >>> np.log2(0.5 - s2) -28.0 >>> s3, t3 = newton_refine(s2, curve1, t2, curve2) >>> s3 == t3 == s2 True
Due to round-off near the point of tangency, the final error resembles \(\sqrt{\varepsilon}\) rather than machine precision as expected.
Parameters: Returns: The refined parameters from a single Newton step.
Return type:
-
bezier._intersection_helpers.segment_intersection(start0, end0, start1, end1)¶ Determine the intersection of two line segments.
Assumes each line is parametric
\[\begin{split}\begin{alignat*}{2} L_0(s) &= S_0 (1 - s) + E_0 s &&= S_0 + s \Delta_0 \\ L_1(t) &= S_1 (1 - t) + E_1 t &&= S_1 + t \Delta_1. \end{alignat*}\end{split}\]To solve \(S_0 + s \Delta_0 = S_1 + t \Delta_1\), we use the cross product:
\[\left(S_0 + s \Delta_0\right) \times \Delta_1 = \left(S_1 + t \Delta_1\right) \times \Delta_1 \Longrightarrow s \left(\Delta_0 \times \Delta_1\right) = \left(S_1 - S_0\right) \times \Delta_1.\]Similarly
\[\Delta_0 \times \left(S_0 + s \Delta_0\right) = \Delta_0 \times \left(S_1 + t \Delta_1\right) \Longrightarrow \left(S_1 - S_0\right) \times \Delta_0 = \Delta_0 \times \left(S_0 - S_1\right) = t \left(\Delta_0 \times \Delta_1\right).\]Note
Since our points are in \(\mathbf{R}^2\), the “traditional” cross-product in \(\mathbf{R}^3\) will always point in the \(z\) direction, so in the above we mean the \(z\) component of the cross product, rather than the entire vector.
For example, the diagonal lines
\[\begin{split}\begin{align*} L_0(s) &= \left[\begin{array}{c} 0 \\ 0 \end{array}\right] (1 - s) + \left[\begin{array}{c} 2 \\ 2 \end{array}\right] s \\ L_1(t) &= \left[\begin{array}{c} -1 \\ 2 \end{array}\right] (1 - t) + \left[\begin{array}{c} 1 \\ 0 \end{array}\right] t \end{align*}\end{split}\]intersect at \(L_0\left(\frac{1}{4}\right) = L_1\left(\frac{3}{4}\right) = \frac{1}{2} \left[\begin{array}{c} 1 \\ 1 \end{array}\right]\).
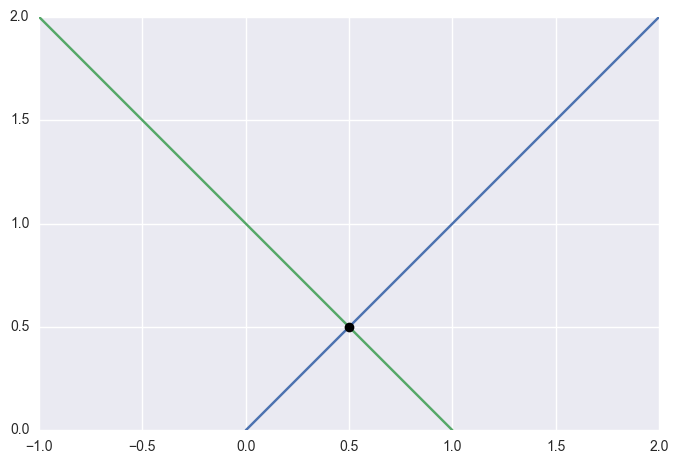
>>> start0 = np.array([[0.0, 0.0]]) >>> end0 = np.array([[2.0, 2.0]]) >>> start1 = np.array([[-1.0, 2.0]]) >>> end1 = np.array([[1.0, 0.0]]) >>> s, t, _ = segment_intersection(start0, end0, start1, end1) >>> s 0.25 >>> t 0.75
Taking the parallel (but different) lines
\[\begin{split}\begin{align*} L_0(s) &= \left[\begin{array}{c} 1 \\ 0 \end{array}\right] (1 - s) + \left[\begin{array}{c} 0 \\ 1 \end{array}\right] s \\ L_1(t) &= \left[\begin{array}{c} -1 \\ 3 \end{array}\right] (1 - t) + \left[\begin{array}{c} 3 \\ -1 \end{array}\right] t \end{align*}\end{split}\]we should be able to determine that the lines don’t intersect, but this function is not meant for that check:
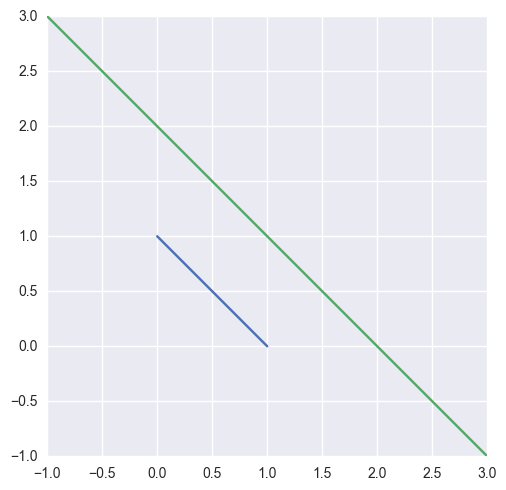
>>> start0 = np.array([[1.0, 0.0]]) >>> end0 = np.array([[0.0, 1.0]]) >>> start1 = np.array([[-1.0, 3.0]]) >>> end1 = np.array([[3.0, -1.0]]) >>> _, _, success = segment_intersection(start0, end0, start1, end1) >>> success False
Instead, we use
parallel_different():>>> parallel_different(start0, end0, start1, end1) True
Parameters: - start0 (numpy.ndarray) – A 1x2 NumPy array that is the start vector \(S_0\) of the parametric line \(L_0(s)\).
- end0 (numpy.ndarray) – A 1x2 NumPy array that is the end vector \(E_0\) of the parametric line \(L_0(s)\).
- start1 (numpy.ndarray) – A 1x2 NumPy array that is the start vector \(S_1\) of the parametric line \(L_1(s)\).
- end1 (numpy.ndarray) – A 1x2 NumPy array that is the end vector \(E_1\) of the parametric line \(L_1(s)\).
Returns: Pair of \(s_{\ast}\) and \(t_{\ast}\) such that the lines intersect: \(L_0\left(s_{\ast}\right) = L_1\left(t_{\ast}\right)\) and then a boolean indicating if an intersection was found.
Return type:
-
bezier._intersection_helpers.parallel_different(start0, end0, start1, end1)¶ Checks if two parallel lines ever meet.
Meant as a back-up when
segment_intersection()fails.Note
This function assumes but never verifies that the lines are parallel.
In the case that the segments are parallel and lie on the exact same line, finding a unique intersection is not possible. However, if they are parallel but on different lines, then there is a guarantee of no intersection.
In
segment_intersection(), we utilized the normal form of the lines (via the cross product):\[\begin{split}\begin{align*} L_0(s) \times \Delta_0 &\equiv S_0 \times \Delta_0 \\ L_1(t) \times \Delta_1 &\equiv S_1 \times \Delta_1 \end{align*}\end{split}\]So, we can detect if \(S_1\) is on the first line by checking if
\[S_0 \times \Delta_0 \stackrel{?}{=} S_1 \times \Delta_0.\]If it is not on the first line, then we are done, the segments don’t meet:
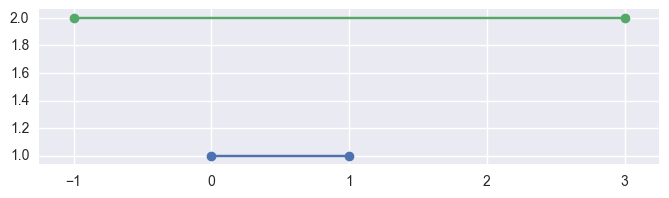
>>> # Line: y = 1 >>> start0 = np.array([[0.0, 1.0]]) >>> end0 = np.array([[1.0, 1.0]]) >>> # Vertical shift up: y = 2 >>> start1 = np.array([[-1.0, 2.0]]) >>> end1 = np.array([[3.0, 2.0]]) >>> parallel_different(start0, end0, start1, end1) True
If \(S_1\) is on the first line, we want to check that \(S_1\) and \(E_1\) define parameters outside of \(\left[0, 1\right]\). To compute these parameters:
\[L_1(t) = S_0 + s_{\ast} \Delta_0 \Longrightarrow s_{\ast} = \frac{\Delta_0^T \left( L_1(t) - S_0\right)}{\Delta_0^T \Delta_0}.\]For example, the intervals \(\left[0, 1\right]\) and \(\left[\frac{3}{2}, 2\right]\) (via \(S_1 = S_0 + \frac{3}{2} \Delta_0\) and \(E_1 = S_0 + 2 \Delta_0\)) correspond to segments that don’t meet:
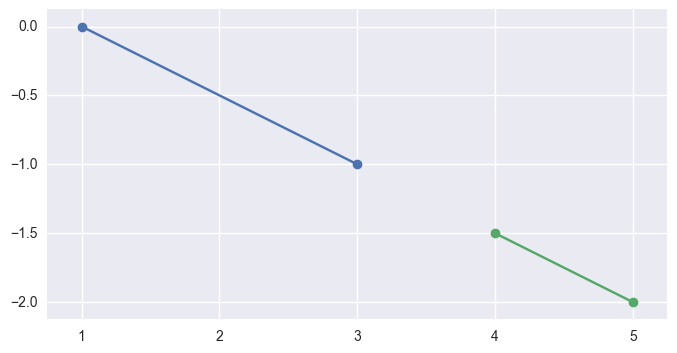
>>> start0 = np.array([[1.0, 0.0]]) >>> delta0 = np.array([[2.0, -1.0]]) >>> end0 = start0 + 1.0 * delta0 >>> start1 = start0 + 1.5 * delta0 >>> end1 = start0 + 2.0 * delta0 >>> parallel_different(start0, end0, start1, end1) True
but if the intervals overlap, like \(\left[0, 1\right]\) and \(\left[-1, \frac{1}{2}\right]\), the segments meet:
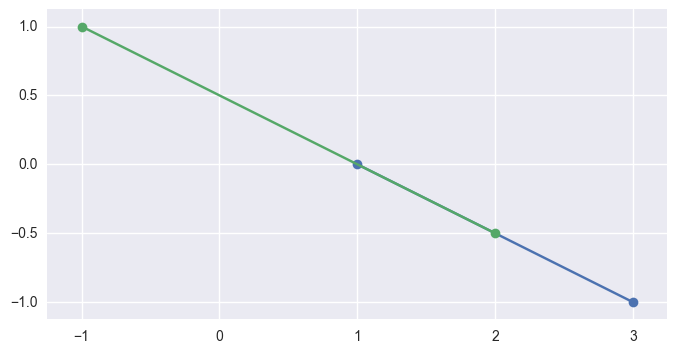
>>> start1 = start0 - 1.0 * delta0 >>> end1 = start0 + 0.5 * delta0 >>> parallel_different(start0, end0, start1, end1) False
Similarly, if the second interval completely contains the first, the segments meet:
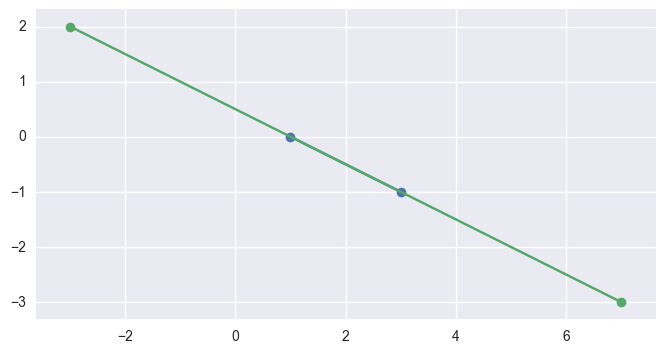
>>> start1 = start0 + 3.0 * delta0 >>> end1 = start0 - 2.0 * delta0 >>> parallel_different(start0, end0, start1, end1) False
Note
This function doesn’t currently allow wiggle room around the desired value, i.e. the two values must be bitwise identical. However, the most “correct” version of this function likely should allow for some round off.
Parameters: - start0 (numpy.ndarray) – A 1x2 NumPy array that is the start vector \(S_0\) of the parametric line \(L_0(s)\).
- end0 (numpy.ndarray) – A 1x2 NumPy array that is the end vector \(E_0\) of the parametric line \(L_0(s)\).
- start1 (numpy.ndarray) – A 1x2 NumPy array that is the start vector \(S_1\) of the parametric line \(L_1(s)\).
- end1 (numpy.ndarray) – A 1x2 NumPy array that is the end vector \(E_1\) of the parametric line \(L_1(s)\).
Returns: Indicating if the lines are different.
Return type:
-
bezier._curve_helpers.get_curvature(nodes, degree, tangent_vec, s)¶ Compute the signed curvature of a curve at \(s\).
Computed via
\[\frac{B'(s) \times B''(s)}{\left\lVert B'(s) \right\rVert_2^3}\]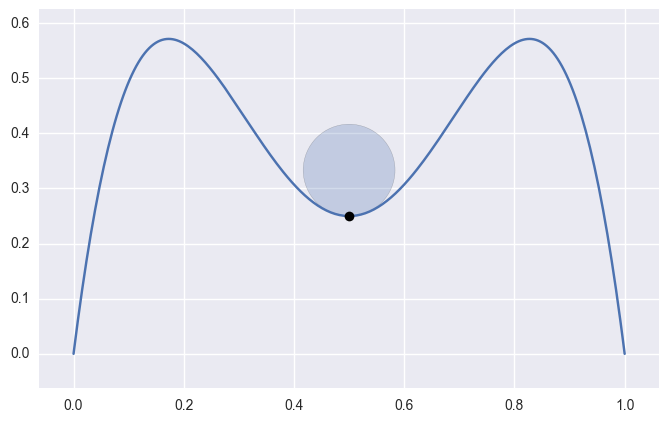
>>> nodes = np.array([ ... [1.0 , 0.0], ... [0.75, 2.0], ... [0.5 , -2.0], ... [0.25, 2.0], ... [0.0 , 0.0], ... ]) >>> s = 0.5 >>> tangent_vec = hodograph(nodes, s) >>> tangent_vec array([-1., 0.]) >>> curvature = get_curvature(nodes, 4, tangent_vec, s) >>> curvature -12.0
Parameters: - nodes (numpy.ndarray) – The nodes of a curve.
- degree (int) – The degree of the curve.
- tangent_vec (numpy.ndarray) – The already computed value of \(B'(s)\)
- s (float) – The parameter value along the curve.
Returns: The signed curvature.
Return type:
-
class
bezier._intersection_helpers.Intersection(left, s, right, t, point=None, at_endpoint=False)¶ Representation of a curve-curve intersection.
Parameters: - left (Curve) – The “left” curve in the intersection.
- s (float) – The parameter along
leftwhere the intersection occurs. - right (Curve) – The “right” curve in the intersection.
- t (float) – The parameter along
rightwhere the intersection occurs. - point (
Optional[numpy.ndarray]) – The point where the two curves actually intersect. If not provided, will be computed on the fly when first accessed. - at_endpoint (bool) – Indicates if the intersection happened at the endpoint of one (or both) of the two subdivided curves. This can be used to help with de-duplication of encountered intersections.
-
left¶ Curve: The “left” curve in the intersection.
-
right¶ Curve: The “right” curve in the intersection.
-
point¶ numpy.ndarray: The point where the intersection occurs.
-
interior_curve¶ int: Which of the curves is on the interior.
Will be
0for theleft,1for therightand-1if it is ambiguous (e.g. the curves are tangent but moving in opposite directions).Raises: AttributeError– If the value has not already been set.
-
class
bezier._intersection_helpers.Linearization(curve, error=None)¶ A linearization of a curve.
This class is provided as a stand-in for a curve, so it provides a similar interface.
Parameters: - curve (Curve) – A curve that is linearized.
- error (
Optional[float]) – The linearization error. If not provided, this value is computed on the fly vialinearization_error().
-
subdivide()¶ Do-nothing method to match the
Curveinterface.Returns: List of all subdivided parts, which is just the current object. Return type: Tuple[Linearization]
-
curve¶ Curve: The curve that this linearization approximates.
-
error¶ float: The linearization error for the linearized curve.
-
start_node¶ numpy.ndarray: The start vector of this linearization.
-
end_node¶ numpy.ndarray: The end vector of this linearization.
-
classmethod
from_shape(shape)¶ Try to linearize a curve (or an already linearized curve).
Parameters: shape ( Union[Curve,Linearization]) – A curve or an already linearized curve.Returns: The (potentially linearized) curve. Return type: Union[Curve,Linearization]
-
bezier._surface_helpers.newton_refine(surface, x_val, y_val, s, t)¶ Refine a solution to \(B(s, t) = p\) using Newton’s method.
Computes updates via
\[\begin{split}\left[\begin{array}{c} 0 \\ 0 \end{array}\right] \approx \left(B\left(s_{\ast}, t_{\ast}\right) - \left[\begin{array}{c} x \\ y \end{array}\right]\right) + \left[\begin{array}{c c} B_s\left(s_{\ast}, t_{\ast}\right) & B_t\left(s_{\ast}, t_{\ast}\right) \end{array}\right] \left[\begin{array}{c} \Delta s \\ \Delta t \end{array}\right]\end{split}\]For example, (with weights \(\lambda_1 = 1 - s - t, \lambda_2 = s, \lambda_3 = t\)) consider the surface
\[\begin{split}B(s, t) = \left[\begin{array}{c} 0 \\ 0 \end{array}\right] \lambda_1^2 + \left[\begin{array}{c} 1 \\ 0 \end{array}\right] 2 \lambda_1 \lambda_2 + \left[\begin{array}{c} 2 \\ 0 \end{array}\right] \lambda_2^2 + \left[\begin{array}{c} 2 \\ 1 \end{array}\right] 2 \lambda_1 \lambda_3 + \left[\begin{array}{c} 2 \\ 2 \end{array}\right] 2 \lambda_2 \lambda_1 + \left[\begin{array}{c} 0 \\ 2 \end{array}\right] \lambda_3^2\end{split}\]and the point \(B\left(\frac{1}{4}, \frac{1}{2}\right) = \frac{1}{4} \left[\begin{array}{c} 5 \\ 5 \end{array}\right]\).
Starting from the wrong point \(s = \frac{1}{2}, t = \frac{1}{4}\), we have
\[\begin{split}\begin{align*} \left[\begin{array}{c} x \\ y \end{array}\right] - B\left(\frac{1}{2}, \frac{1}{4}\right) &= \frac{1}{4} \left[\begin{array}{c} -1 \\ 2 \end{array}\right] \\ DB\left(\frac{1}{2}, \frac{1}{4}\right) &= \frac{1}{2} \left[\begin{array}{c c} 3 & 2 \\ 1 & 6 \end{array}\right] \\ \Longrightarrow \left[\begin{array}{c} \Delta s \\ \Delta t \end{array}\right] &= \frac{1}{32} \left[\begin{array}{c} -10 \\ 7 \end{array}\right] \end{align*}\end{split}\]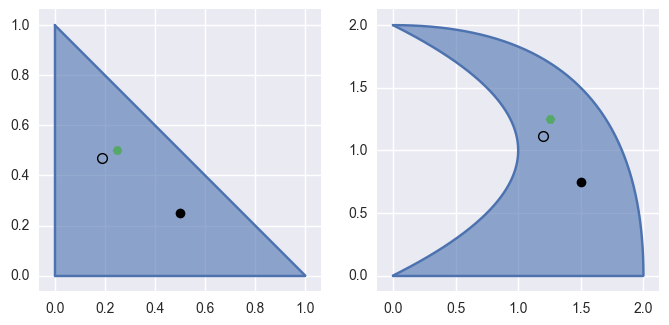
>>> surface = bezier.Surface(np.array([ ... [0.0, 0.0], ... [1.0, 0.0], ... [2.0, 0.0], ... [2.0, 1.0], ... [2.0, 2.0], ... [0.0, 2.0], ... ])) >>> surface.is_valid True >>> x_val, y_val = surface.evaluate_cartesian(0.25, 0.5) >>> x_val, y_val (1.25, 1.25) >>> s, t = 0.5, 0.25 >>> new_s, new_t = newton_refine(surface, x_val, y_val, s, t) >>> 32 * (new_s - s) -10.0 >>> 32 * (new_t - t) 7.0
Parameters: Returns: The refined \(s\) and \(t\) values.
Return type:
-
bezier._surface_helpers.classify_intersection(intersection)¶ Determine which curve is on the “inside of the intersection”.
This is intended to be a helper for forming a
CurvedPolygonfrom the edge intersections of twoSurface-s. In order to move from one intersection to another (or to the end of an edge), the interior edge must be determined at the point of intersection.The “typical” case is on the interior of both edges:
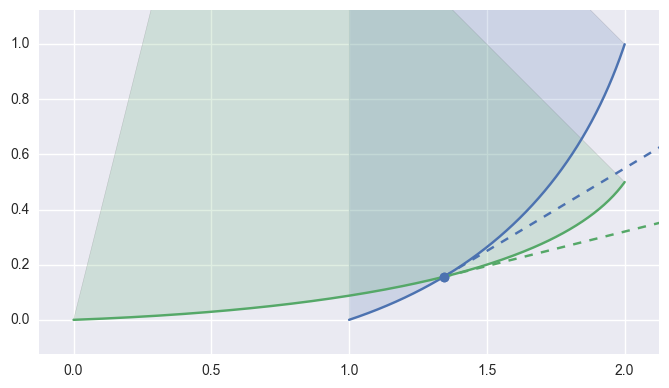
>>> curve1 = bezier.Curve(np.array([ ... [1.0 , 0.0 ], ... [1.75, 0.25], ... [2.0 , 1.0 ], ... ])) >>> curve2 = bezier.Curve(np.array([ ... [0.0 , 0.0 ], ... [1.6875, 0.0625], ... [2.0 , 0.5 ], ... ])) >>> s, t = 0.25, 0.5 >>> curve1.evaluate(s) == curve2.evaluate(t) array([ True, True], dtype=bool) >>> tangent1 = hodograph(curve1, s) >>> tangent1 array([ 1.25, 0.75]) >>> tangent2 = hodograph(curve2, t) >>> tangent2 array([ 2. , 0.5]) >>> intersection = Intersection(curve1, s, curve2, t) >>> classify_intersection(intersection) <IntersectionClassification.first: 'first'>
We determine the interior / left one by using the right-hand rule: by embedding the tangent vectors in \(\mathbf{R}^3\), we compute
\[\begin{split}\left[\begin{array}{c} x_1'(s) \\ y_1'(s) \\ 0 \end{array}\right] \times \left[\begin{array}{c} x_2'(t) \\ y_2'(t) \\ 0 \end{array}\right] = \left[\begin{array}{c} 0 \\ 0 \\ x_1'(s) y_2'(t) - x_2'(t) y_1'(s) \end{array}\right].\end{split}\]If the cross-product quantity \(B_1'(s) \times B_2'(t) = x_1'(s) y_2'(t) - x_2'(t) y_1'(s)\) is positive, then the first curve is “to the right”, i.e. the second curve is interior. If the cross-product is negative, the first curve is interior.
When \(B_1'(s) \times B_2'(t) = 0\), the tangent vectors are parallel, i.e. the intersection is a point of tangency:
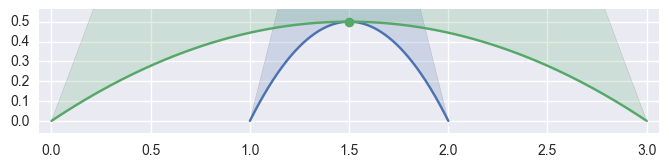
>>> curve1 = bezier.Curve(np.array([ ... [1.0, 0.0], ... [1.5, 1.0], ... [2.0, 0.0], ... ])) >>> curve2 = bezier.Curve(np.array([ ... [0.0, 0.0], ... [1.5, 1.0], ... [3.0, 0.0], ... ])) >>> s, t = 0.5, 0.5 >>> curve1.evaluate(s) == curve2.evaluate(t) array([ True, True], dtype=bool) >>> intersection = Intersection(curve1, s, curve2, t) >>> classify_intersection(intersection) <IntersectionClassification.tangent_second: 'tangent_second'>
Depending on the direction of the parameterizations, the interior curve may change, but we can use the (signed) curvature of each curve at that point to determine which is on the interior:
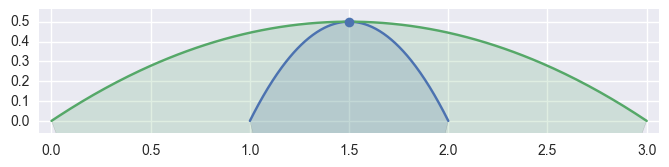
>>> curve1 = bezier.Curve(np.array([ ... [2.0, 0.0], ... [1.5, 1.0], ... [1.0, 0.0], ... ])) >>> curve2 = bezier.Curve(np.array([ ... [3.0, 0.0], ... [1.5, 1.0], ... [0.0, 0.0], ... ])) >>> s, t = 0.5, 0.5 >>> curve1.evaluate(s) == curve2.evaluate(t) array([ True, True], dtype=bool) >>> intersection = Intersection(curve1, s, curve2, t) >>> classify_intersection(intersection) <IntersectionClassification.tangent_first: 'tangent_first'>
When the curves are moving in opposite directions at a point of tangency, there is no side to choose. Either the point of tangency is not part of any
CurvedPolygonintersection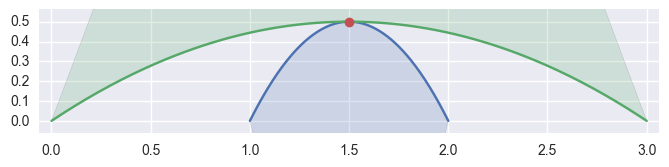
>>> curve1 = bezier.Curve(np.array([ ... [2.0, 0.0], ... [1.5, 1.0], ... [1.0, 0.0], ... ])) >>> curve2 = bezier.Curve(np.array([ ... [0.0, 0.0], ... [1.5, 1.0], ... [3.0, 0.0], ... ])) >>> s, t = 0.5, 0.5 >>> curve1.evaluate(s) == curve2.evaluate(t) array([ True, True], dtype=bool) >>> intersection = Intersection(curve1, s, curve2, t) >>> classify_intersection(intersection) <IntersectionClassification.opposed: 'opposed'>
or the point of tangency is a “degenerate” part of two
CurvedPolygonintersections. It is “degenerate” because from one direction, the point should be classified as1and from another as0: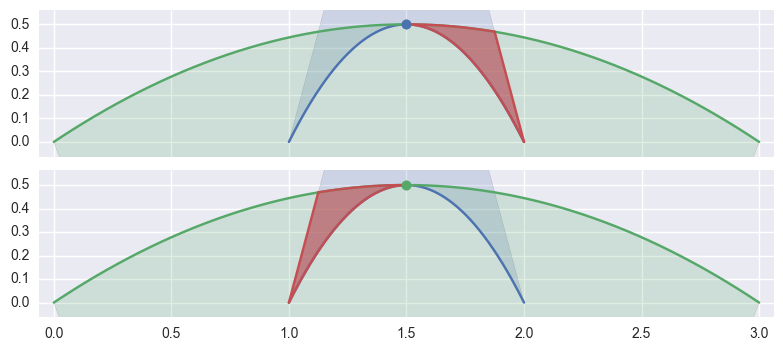
>>> curve1 = bezier.Curve(np.array([ ... [1.0, 0.0], ... [1.5, 1.0], ... [2.0, 0.0], ... ])) >>> curve2 = bezier.Curve(np.array([ ... [3.0, 0.0], ... [1.5, 1.0], ... [0.0, 0.0], ... ])) >>> s, t = 0.5, 0.5 >>> curve1.evaluate(s) == curve2.evaluate(t) array([ True, True], dtype=bool) >>> intersection = Intersection(curve1, s, curve2, t) >>> classify_intersection(intersection) Traceback (most recent call last): ... NotImplementedError: Curves moving in opposite direction but define overlapping arcs.
However, if the curvature of each curve is identical, we don’t try to distinguish further:
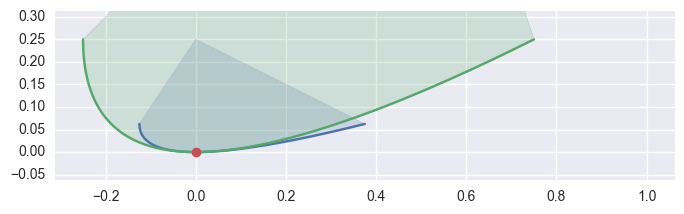
>>> curve1 = bezier.Curve(np.array([ ... [ 0.375, 0.0625], ... [-0.125, -0.0625], ... [-0.125, 0.0625], ... ])) >>> curve2 = bezier.Curve(np.array([ ... [ 0.75, 0.25], ... [-0.25, -0.25], ... [-0.25, 0.25], ... ])) >>> s, t = 0.5, 0.5 >>> curve1.evaluate(s) == curve2.evaluate(t) array([ True, True], dtype=bool) >>> hodograph(curve1, s) array([-0.5, 0. ]) >>> hodograph(curve2, t) array([-1., 0.]) >>> curvature(curve1, s) -2.0 >>> curvature(curve2, t) -2.0 >>> intersection = Intersection(curve1, s, curve2, t) >>> classify_intersection(intersection) Traceback (most recent call last): ... NotImplementedError: Tangent curves have same curvature.
In addition to points of tangency, intersections that happen at the end of an edge need special handling:
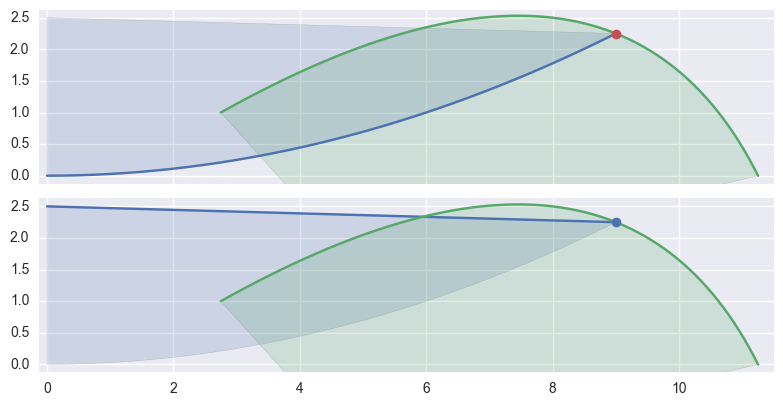
>>> curve1a = bezier.Curve(np.array([ ... [0.0, 0.0 ], ... [4.5, 0.0 ], ... [9.0, 2.25], ... ])) >>> curve2 = bezier.Curve(np.array([ ... [11.25, 0.0], ... [ 9.0 , 4.5], ... [ 2.75, 1.0], ... ])) >>> s, t = 1.0, 0.375 >>> curve1a.evaluate(s) == curve2.evaluate(t) array([ True, True], dtype=bool) >>> intersection = Intersection(curve1a, s, curve2, t) >>> classify_intersection(intersection) Traceback (most recent call last): ... ValueError: ('Intersection occurs at the end of an edge', 's', 1.0, 't', 0.375) >>> >>> curve1b = bezier.Curve(np.array([ ... [9.0, 2.25 ], ... [4.5, 2.375], ... [0.0, 2.5 ], ... ])) >>> curve1b.evaluate(0.0) == curve2.evaluate(t) array([ True, True], dtype=bool) >>> intersection = Intersection(curve1b, 0.0, curve2, t) >>> classify_intersection(intersection) <IntersectionClassification.first: 'first'>
Note
This assumes the intersection occurs in \(\mathbf{R}^2\) but doesn’t check this.
Note
This function doesn’t allow wiggle room / round-off when checking endpoints, nor when checking if the cross-product is near zero, nor when curvatures are compared. However, the most “correct” version of this function likely should allow for some round off.
Parameters: intersection (Intersection) – An intersection object. Returns: The “inside” curve type, based on the classification enum. Return type: IntersectionClassification Raises: ValueError– If the intersection occurs at the end of either curve involved. This is because we want to classify which curve to move forward on, and we can’t move past the end of a segment.