bezier.hazmat.triangle_helpers module¶
Pure Python helper methods for bezier.triangle.
- bezier.hazmat.triangle_helpers.polynomial_sign(poly_triangle, degree)¶
Determine the “sign” of a polynomial on the reference triangle.
Note
This is used only by
Triangle._compute_valid()(which is in turn used to compute / cache theTriangle.is_validproperty).Checks if a polynomial \(p(s, t)\) is positive, negative or mixed sign on the reference triangle.
Does this by utilizing the Bézier form of \(p\): it is a convex combination of the Bernstein basis (real numbers) hence if the Bernstein basis is all positive, the polynomial must be.
If the values are mixed, then we can recursively subdivide until we are in a region where the coefficients are all one sign.
- Parameters:
poly_triangle (numpy.ndarray) – 2D array (with 1 row) of control points for a “triangle”, i.e. a bivariate polynomial.
degree (int) – The degree of the triangle / polynomial given by
poly_triangle.
- Returns:
The sign of the polynomial. Will be one of
-1,1or0. A value of0indicates a mixed sign or the zero polynomial.- Return type:
- Raises:
ValueError – If no conclusion is reached after the maximum number of subdivisions.
- bezier.hazmat.triangle_helpers.two_by_two_det(mat)¶
Compute the determinant of a 2x2 matrix.
Note
This is used only by
quadratic_jacobian_polynomial()andcubic_jacobian_polynomial().This is “needed” because
numpy.linalg.det()uses a more generic determinant implementation which can introduce rounding even when the simple \(a d - b c\) will suffice. For example:- Parameters:
mat (numpy.ndarray) – A 2x2 matrix.
- Returns:
The determinant of
mat.- Return type:
- bezier.hazmat.triangle_helpers.quadratic_jacobian_polynomial(nodes)¶
Compute the Jacobian determinant of a quadratic triangle.
Note
This is used only by
Triangle._compute_valid()(which is in turn used to compute / cache theTriangle.is_validproperty).Converts \(\det(J(s, t))\) to a polynomial on the reference triangle and represents it as a triangle object.
Note
This assumes that
nodesis2 x 6but doesn’t verify this. (However, the right multiplication by_QUADRATIC_JACOBIAN_HELPERwould fail ifnodeswasn’tR x 6and then the ensuing determinants would fail if there weren’t 2 rows.)- Parameters:
nodes (numpy.ndarray) – A 2 x 6 array of nodes in a triangle.
- Returns:
1 x 6 array, coefficients in Bernstein basis.
- Return type:
- bezier.hazmat.triangle_helpers.cubic_jacobian_polynomial(nodes)¶
Compute the Jacobian determinant of a cubic triangle.
Note
This is used only by
Triangle._compute_valid()(which is in turn used to compute / cache theTriangle.is_validproperty).Converts \(\det(J(s, t))\) to a polynomial on the reference triangle and represents it as a triangle object.
Note
This assumes that
nodesis2 x 10but doesn’t verify this. (However, the right multiplication by_CUBIC_JACOBIAN_HELPERwould fail ifnodeswasn’tR x 10and then the ensuing determinants would fail if there weren’t 2 rows.)- Parameters:
nodes (numpy.ndarray) – A 2 x 10 array of nodes in a triangle.
- Returns:
1 x 15 array, coefficients in Bernstein basis.
- Return type:
- bezier.hazmat.triangle_helpers.de_casteljau_one_round(nodes, degree, lambda1, lambda2, lambda3)¶
Performs one “round” of the de Casteljau algorithm for triangles.
Note
There is also a Fortran implementation of this function, which will be used if it can be built.
Note
This is a helper function, used by
make_transform()andspecialize_triangle()(andmake_transform()is only used byspecialize_triangle()).Converts the
nodesinto a basis for a triangle one degree smaller by using the barycentric weights:\[q_{i, j, k} = \lambda_1 \cdot p_{i + 1, j, k} + \lambda_2 \cdot p_{i, j + 1, k} + \lambda_2 \cdot p_{i, j, k + 1}\]- Parameters:
nodes (numpy.ndarray) – The nodes to reduce.
degree (int) – The degree of the triangle.
lambda1 (float) – Parameter along the reference triangle.
lambda2 (float) – Parameter along the reference triangle.
lambda3 (float) – Parameter along the reference triangle.
- Returns:
The converted nodes.
- Return type:
- bezier.hazmat.triangle_helpers.make_transform(degree, weights_a, weights_b, weights_c)¶
Compute matrices corresponding to the de Casteljau algorithm.
Note
This is a helper used only by
specialize_triangle().Applies the de Casteljau algorithm to the identity matrix, thus effectively caching the algorithm in a transformation matrix.
Note
This is premature optimization. It’s unclear if the time saved from “caching” one round of de Casteljau is cancelled out by the extra storage required for the 3 matrices.
- Parameters:
degree (int) – The degree of a candidate triangle.
weights_a (numpy.ndarray) – Triple (1D array) of barycentric weights for a point in the reference triangle
weights_b (numpy.ndarray) – Triple (1D array) of barycentric weights for a point in the reference triangle
weights_c (numpy.ndarray) – Triple (1D array) of barycentric weights for a point in the reference triangle
- Returns:
Mapping from keys to the de Casteljau transformation mappings. The keys are
0corresponding toweights_a,1toweights_band2toweights_c.- Return type:
- bezier.hazmat.triangle_helpers.reduced_to_matrix(shape, degree, vals_by_weight)¶
Converts a reduced values dictionary into a matrix.
Note
This is a helper used only by
specialize_triangle().The
vals_by_weightmapping has keys of the form:(0, ..., 1, ..., 2, ...)where the0corresponds to the number of times the first set of barycentric weights was used in the reduction process, and similarly for1and2.These points correspond to barycentric weights in their own right. For example
(0, 0, 0, 1, 2, 2)corresponds to the barycentric weight \(\left(\frac{3}{6}, \frac{1}{6}, \frac{2}{6}\right)\).Once the keys in
vals_by_weighthave been converted to barycentric coordinates, we order them according to our rule (bottom to top, left to right) and then return them in a single matrix.- Parameters:
shape (tuple) – The shape of the result matrix.
degree (int) – The degree of the triangle.
vals_by_weight (
Mappingtuple,numpy.ndarray) – Dictionary of reduced nodes according to blending of each of the three sets of weights in a reduction.
- Returns:
The newly created reduced control points.
- Return type:
- bezier.hazmat.triangle_helpers.specialize_triangle(nodes, degree, weights_a, weights_b, weights_c)¶
Specialize a triangle to a reparameterization.
Note
There is also a Fortran implementation of this function, which will be used if it can be built.
Does so by taking three points (in barycentric form) within the reference triangle and then reparameterizing the triangle onto the triangle formed by those three points.
Note
This assumes the triangle is degree 1 or greater but doesn’t check.
Note
This is used only as a helper for
subdivide_nodes(), however it may be worth adding this toTriangleas an analogue toCurve.specialize().- Parameters:
nodes (numpy.ndarray) – Control points for a triangle.
degree (int) – The degree of the triangle.
weights_a (numpy.ndarray) – Triple (1D array) of barycentric weights for a point in the reference triangle
weights_b (numpy.ndarray) – Triple (1D array) of barycentric weights for a point in the reference triangle
weights_c (numpy.ndarray) – Triple (1D array) of barycentric weights for a point in the reference triangle
- Returns:
The control points for the specialized triangle.
- Return type:
- bezier.hazmat.triangle_helpers.subdivide_nodes(nodes, degree)¶
Subdivide a triangle into four sub-triangles.
Note
There is also a Fortran implementation of this function, which will be used if it can be built.
Does so by taking the unit triangle (i.e. the domain of the triangle) and splitting it into four sub-triangles by connecting the midpoints of each side.
- Parameters:
nodes (numpy.ndarray) – Control points for a triangle.
degree (int) – The degree of the triangle.
- Returns:
The nodes for the four sub-triangles.
- Return type:
Tuplenumpy.ndarray,numpy.ndarray,numpy.ndarray,numpy.ndarray
- bezier.hazmat.triangle_helpers.jacobian_s(nodes, degree, dimension)¶
Compute \(\frac{\partial B}{\partial s}\).
Note
This is a helper for
jacobian_both(), which has an equivalent Fortran implementation.- Parameters:
nodes (numpy.ndarray) – Array of nodes in a triangle.
degree (int) – The degree of the triangle.
dimension (int) – The dimension the triangle lives in.
- Returns:
Nodes of the Jacobian triangle in Bézier form.
- Return type:
- bezier.hazmat.triangle_helpers.jacobian_t(nodes, degree, dimension)¶
Compute \(\frac{\partial B}{\partial t}\).
Note
This is a helper for
jacobian_both(), which has an equivalent Fortran implementation.- Parameters:
nodes (numpy.ndarray) – Array of nodes in a triangle.
degree (int) – The degree of the triangle.
dimension (int) – The dimension the triangle lives in.
- Returns:
Nodes of the Jacobian triangle in Bézier form.
- Return type:
- bezier.hazmat.triangle_helpers.jacobian_both(nodes, degree, dimension)¶
Compute \(s\) and \(t\) partial of \(B\).
Note
There is also a Fortran implementation of this function, which will be used if it can be built.
- Parameters:
nodes (numpy.ndarray) – Array of nodes in a triangle.
degree (int) – The degree of the triangle.
dimension (int) – The dimension the triangle lives in.
- Returns:
Nodes of the Jacobian triangles in Bézier form.
- Return type:
- bezier.hazmat.triangle_helpers.jacobian_det(nodes, degree, st_vals)¶
Compute \(\det(D B)\) at a set of values.
This requires that \(B \in \mathbf{R}^2\).
Note
This assumes but does not check that each
(s, t)inst_valsis inside the reference triangle.Warning
This relies on helpers in
bezierfor computing the Jacobian of the triangle. However, these helpers are not part of the public API and may change or be removed.>>> import bezier >>> import numpy as np >>> nodes = np.asfortranarray([ ... [0.0, 1.0, 2.0, 0.0, 1.5, 0.0], ... [0.0, 0.0, 0.0, 1.0, 1.5, 2.0], ... ]) >>> triangle = bezier.Triangle(nodes, degree=2) >>> st_vals = np.asfortranarray([ ... [0.25, 0.0 ], ... [0.75, 0.125], ... [0.5 , 0.5 ], ... ]) >>> s_vals, t_vals = st_vals.T >>> triangle.evaluate_cartesian_multi(st_vals) array([[0.5 , 1.59375, 1.25 ], [0. , 0.34375, 1.25 ]]) >>> # B(s, t) = [s(t + 2), t(s + 2)] >>> s_vals * (t_vals + 2) array([0.5 , 1.59375, 1.25 ]) >>> t_vals * (s_vals + 2) array([0. , 0.34375, 1.25 ]) >>> jacobian_det(nodes, 2, st_vals) array([4.5 , 5.75, 6. ]) >>> # det(DB) = 2(s + t + 2) >>> 2 * (s_vals + t_vals + 2) array([4.5 , 5.75, 6. ])
Note
There is also a Fortran implementation of this function, which will be used if it can be built.
- Parameters:
nodes (numpy.ndarray) – Nodes defining a Bézier triangle \(B(s, t)\).
degree (int) – The degree of the triangle \(B\).
st_vals (numpy.ndarray) –
N x 2array of Cartesian inputs to Bézier triangles defined by \(B_s\) and \(B_t\).
- Returns:
Array of all determinant values, one for each row in
st_vals.- Return type:
- bezier.hazmat.triangle_helpers.classify_tangent_intersection(intersection, nodes1, tangent1, nodes2, tangent2)¶
Helper for
classify_intersection()at tangencies.Note
This is a helper used only by
classify_intersection().- Parameters:
intersection (Intersection) – An intersection object.
nodes1 (numpy.ndarray) – Control points for the first curve at the intersection.
tangent1 (numpy.ndarray) – The tangent vector to the first curve at the intersection (
2 x 1array).nodes2 (numpy.ndarray) – Control points for the second curve at the intersection.
tangent2 (numpy.ndarray) – The tangent vector to the second curve at the intersection (
2 x 1array).
- Returns:
The “inside” curve type, based on the classification enum. Will either be
opposedor one of thetangentvalues.- Return type:
- Raises:
NotImplementedError – If the curves are tangent at the intersection and have the same curvature.
- bezier.hazmat.triangle_helpers.ignored_edge_corner(edge_tangent, corner_tangent, corner_previous_edge)¶
Check ignored when a corner lies inside another edge.
Note
This is a helper used only by
ignored_corner(), which in turn is only used byclassify_intersection().Helper for
ignored_corner()where one ofsandtare0, but not both.- Parameters:
edge_tangent (numpy.ndarray) – Tangent vector (
2 x 1array) along the edge that the intersection occurs in the middle of.corner_tangent (numpy.ndarray) – Tangent vector (
2 x 1array) at the corner where intersection occurs (at the beginning of edge).corner_previous_edge (numpy.ndarray) – Edge that ends at the corner intersection (whereas
corner_tangentcomes from the edge that begins at the corner intersection). This is a2 x Narray whereNis the number of nodes on the edge.
- Returns:
Indicates if the corner intersection should be ignored.
- Return type:
- bezier.hazmat.triangle_helpers.ignored_double_corner(intersection, tangent_s, tangent_t, edge_nodes1, edge_nodes2)¶
Check if an intersection is an “ignored” double corner.
Note
This is a helper used only by
ignored_corner(), which in turn is only used byclassify_intersection().Helper for
ignored_corner()where bothsandtare0.Does so by checking if either edge through the
tcorner goes through the interior of the other triangle. An interior check is done by checking that a few cross products are positive.- Parameters:
intersection (Intersection) – An intersection to “diagnose”.
tangent_s (numpy.ndarray) – The tangent vector (
2 x 1array) to the first curve at the intersection.tangent_t (numpy.ndarray) – The tangent vector (
2 x 1array) to the second curve at the intersection.edge_nodes1 (
Tuplenumpy.ndarray,numpy.ndarray,numpy.ndarray) – The nodes of the three edges of the first triangle being intersected.edge_nodes2 (
Tuplenumpy.ndarray,numpy.ndarray,numpy.ndarray) – The nodes of the three edges of the second triangle being intersected.
- Returns:
Indicates if the corner is to be ignored.
- Return type:
- bezier.hazmat.triangle_helpers.ignored_corner(intersection, tangent_s, tangent_t, edge_nodes1, edge_nodes2)¶
Check if an intersection is an “ignored” corner.
Note
This is a helper used only by
classify_intersection().An “ignored” corner is one where the triangles just “kiss” at the point of intersection but their interiors do not meet.
We can determine this by comparing the tangent lines from the point of intersection.
Note
This assumes the
intersectionhas been shifted to the beginning of a curve so only checks ifs == 0.0ort == 0.0(rather than also checking for1.0).- Parameters:
intersection (Intersection) – An intersection to “diagnose”.
tangent_s (numpy.ndarray) – The tangent vector (
2 x 1array) to the first curve at the intersection.tangent_t (numpy.ndarray) – The tangent vector (
2 x 1array) to the second curve at the intersection.edge_nodes1 (
Tuplenumpy.ndarray,numpy.ndarray,numpy.ndarray) – The nodes of the three edges of the first triangle being intersected.edge_nodes2 (
Tuplenumpy.ndarray,numpy.ndarray,numpy.ndarray) – The nodes of the three edges of the second triangle being intersected.
- Returns:
Indicates if the corner is to be ignored.
- Return type:
- bezier.hazmat.triangle_helpers.classify_intersection(intersection, edge_nodes1, edge_nodes2)¶
Determine which curve is on the “inside of the intersection”.
Note
This is a helper used only by
Triangle.intersect().This is intended to be a helper for forming a
CurvedPolygonfrom the edge intersections of twoTriangle-s. In order to move from one intersection to another (or to the end of an edge), the interior edge must be determined at the point of intersection.The “typical” case is on the interior of both edges:
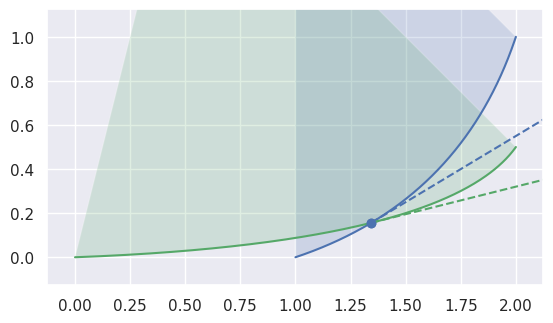
>>> nodes1 = np.asfortranarray([ ... [1.0, 1.75, 2.0], ... [0.0, 0.25, 1.0], ... ]) >>> curve1 = bezier.Curve(nodes1, degree=2) >>> nodes2 = np.asfortranarray([ ... [0.0, 1.6875, 2.0], ... [0.0, 0.0625, 0.5], ... ]) >>> curve2 = bezier.Curve(nodes2, degree=2) >>> s, t = 0.25, 0.5 >>> curve1.evaluate(s) == curve2.evaluate(t) array([[ True], [ True]]) >>> tangent1 = hodograph(curve1, s) >>> tangent1 array([[1.25], [0.75]]) >>> tangent2 = hodograph(curve2, t) >>> tangent2 array([[2. ], [0.5]]) >>> intersection = Intersection(0, s, 0, t) >>> edge_nodes1 = (nodes1, None, None) >>> edge_nodes2 = (nodes2, None, None) >>> classify_intersection(intersection, edge_nodes1, edge_nodes2) <IntersectionClassification.FIRST: 0>
We determine the interior (i.e. left) one by using the right-hand rule: by embedding the tangent vectors in \(\mathbf{R}^3\), we compute
\[\begin{split}\left[\begin{array}{c} x_1'(s) \\ y_1'(s) \\ 0 \end{array}\right] \times \left[\begin{array}{c} x_2'(t) \\ y_2'(t) \\ 0 \end{array}\right] = \left[\begin{array}{c} 0 \\ 0 \\ x_1'(s) y_2'(t) - x_2'(t) y_1'(s) \end{array}\right].\end{split}\]If the cross product quantity \(B_1'(s) \times B_2'(t) = x_1'(s) y_2'(t) - x_2'(t) y_1'(s)\) is positive, then the first curve is “outside” / “to the right”, i.e. the second curve is interior. If the cross product is negative, the first curve is interior.
When \(B_1'(s) \times B_2'(t) = 0\), the tangent vectors are parallel, i.e. the intersection is a point of tangency:
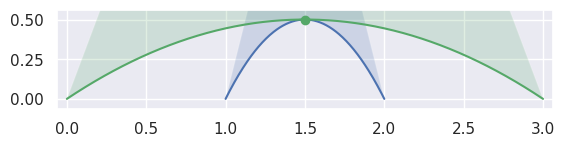
>>> nodes1 = np.asfortranarray([ ... [1.0, 1.5, 2.0], ... [0.0, 1.0, 0.0], ... ]) >>> curve1 = bezier.Curve(nodes1, degree=2) >>> nodes2 = np.asfortranarray([ ... [0.0, 1.5, 3.0], ... [0.0, 1.0, 0.0], ... ]) >>> curve2 = bezier.Curve(nodes2, degree=2) >>> s, t = 0.5, 0.5 >>> curve1.evaluate(s) == curve2.evaluate(t) array([[ True], [ True]]) >>> intersection = Intersection(0, s, 0, t) >>> edge_nodes1 = (nodes1, None, None) >>> edge_nodes2 = (nodes2, None, None) >>> classify_intersection(intersection, edge_nodes1, edge_nodes2) <IntersectionClassification.TANGENT_SECOND: 4>
Depending on the direction of the parameterizations, the interior curve may change, but we can use the (signed) curvature of each curve at that point to determine which is on the interior:
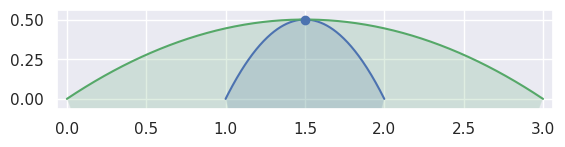
>>> nodes1 = np.asfortranarray([ ... [2.0, 1.5, 1.0], ... [0.0, 1.0, 0.0], ... ]) >>> curve1 = bezier.Curve(nodes1, degree=2) >>> nodes2 = np.asfortranarray([ ... [3.0, 1.5, 0.0], ... [0.0, 1.0, 0.0], ... ]) >>> curve2 = bezier.Curve(nodes2, degree=2) >>> s, t = 0.5, 0.5 >>> curve1.evaluate(s) == curve2.evaluate(t) array([[ True], [ True]]) >>> intersection = Intersection(0, s, 0, t) >>> edge_nodes1 = (nodes1, None, None) >>> edge_nodes2 = (nodes2, None, None) >>> classify_intersection(intersection, edge_nodes1, edge_nodes2) <IntersectionClassification.TANGENT_FIRST: 3>
When the curves are moving in opposite directions at a point of tangency, there is no side to choose. Either the point of tangency is not part of any
CurvedPolygonintersection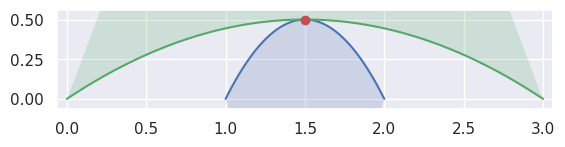
>>> nodes1 = np.asfortranarray([ ... [2.0, 1.5, 1.0], ... [0.0, 1.0, 0.0], ... ]) >>> curve1 = bezier.Curve(nodes1, degree=2) >>> nodes2 = np.asfortranarray([ ... [0.0, 1.5, 3.0], ... [0.0, 1.0, 0.0], ... ]) >>> curve2 = bezier.Curve(nodes2, degree=2) >>> s, t = 0.5, 0.5 >>> curve1.evaluate(s) == curve2.evaluate(t) array([[ True], [ True]]) >>> intersection = Intersection(0, s, 0, t) >>> edge_nodes1 = (nodes1, None, None) >>> edge_nodes2 = (nodes2, None, None) >>> classify_intersection(intersection, edge_nodes1, edge_nodes2) <IntersectionClassification.OPPOSED: 2>
or the point of tangency is a “degenerate” part of two
CurvedPolygonintersections. It is “degenerate” because from one direction, the point should be classified asFIRSTand from another asSECOND.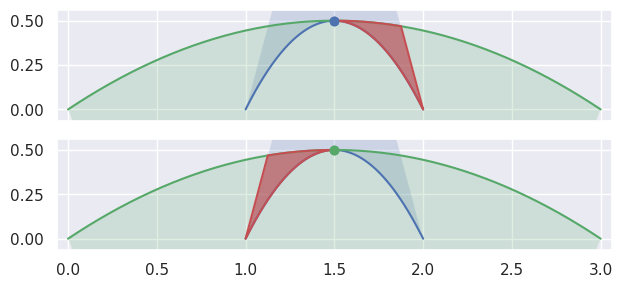
>>> nodes1 = np.asfortranarray([ ... [1.0, 1.5, 2.0], ... [0.0, 1.0, 0.0], ... ]) >>> curve1 = bezier.Curve(nodes1, degree=2) >>> nodes2 = np.asfortranarray([ ... [3.0, 1.5, 0.0], ... [0.0, 1.0, 0.0], ... ]) >>> curve2 = bezier.Curve(nodes2, degree=2) >>> s, t = 0.5, 0.5 >>> curve1.evaluate(s) == curve2.evaluate(t) array([[ True], [ True]]) >>> intersection = Intersection(0, s, 0, t) >>> edge_nodes1 = (nodes1, None, None) >>> edge_nodes2 = (nodes2, None, None) >>> classify_intersection(intersection, edge_nodes1, edge_nodes2) <IntersectionClassification.TANGENT_BOTH: 6>
The
TANGENT_BOTHclassification can also occur if the curves are “kissing” but share a zero width interior at the point of tangency: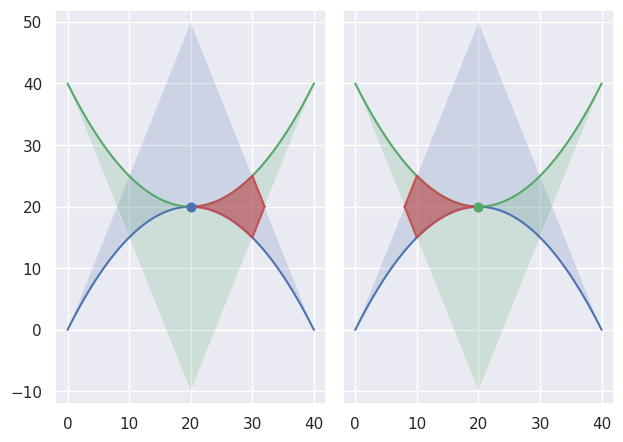
>>> nodes1 = np.asfortranarray([ ... [0.0, 20.0, 40.0], ... [0.0, 40.0, 0.0], ... ]) >>> curve1 = bezier.Curve(nodes1, degree=2) >>> nodes2 = np.asfortranarray([ ... [40.0, 20.0, 0.0], ... [40.0, 0.0, 40.0], ... ]) >>> curve2 = bezier.Curve(nodes2, degree=2) >>> s, t = 0.5, 0.5 >>> curve1.evaluate(s) == curve2.evaluate(t) array([[ True], [ True]]) >>> intersection = Intersection(0, s, 0, t) >>> edge_nodes1 = (nodes1, None, None) >>> edge_nodes2 = (nodes2, None, None) >>> classify_intersection(intersection, edge_nodes1, edge_nodes2) <IntersectionClassification.TANGENT_BOTH: 6>
However, if the curvature of each curve is identical, we don’t try to distinguish further:
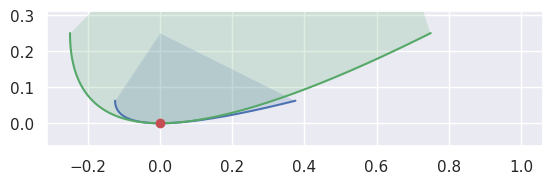
>>> nodes1 = np.asfortranarray([ ... [-0.125 , -0.125 , 0.375 ], ... [ 0.0625, -0.0625, 0.0625], ... ]) >>> curve1 = bezier.Curve(nodes1, degree=2) >>> nodes2 = np.asfortranarray([ ... [-0.25, -0.25, 0.75], ... [ 0.25, -0.25, 0.25], ... ]) >>> curve2 = bezier.Curve(nodes2, degree=2) >>> s, t = 0.5, 0.5 >>> curve1.evaluate(s) == curve2.evaluate(t) array([[ True], [ True]]) >>> hodograph(curve1, s) array([[0.5], [0. ]]) >>> hodograph(curve2, t) array([[1.], [0.]]) >>> curvature(curve1, s) 2.0 >>> curvature(curve2, t) 2.0 >>> intersection = Intersection(0, s, 0, t) >>> edge_nodes1 = (nodes1, None, None) >>> edge_nodes2 = (nodes2, None, None) >>> classify_intersection(intersection, edge_nodes1, edge_nodes2) Traceback (most recent call last): ... NotImplementedError: Tangent curves have same curvature.
In addition to points of tangency, intersections that happen at the end of an edge need special handling:
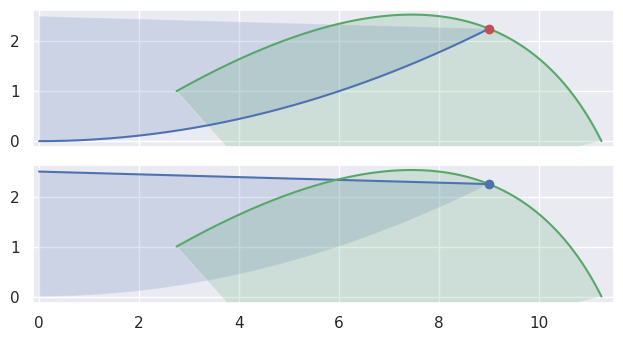
>>> nodes1a = np.asfortranarray([ ... [0.0, 4.5, 9.0 ], ... [0.0, 0.0, 2.25], ... ]) >>> curve1a = bezier.Curve(nodes1a, degree=2) >>> nodes2 = np.asfortranarray([ ... [11.25, 9.0, 2.75], ... [ 0.0 , 4.5, 1.0 ], ... ]) >>> curve2 = bezier.Curve(nodes2, degree=2) >>> s, t = 1.0, 0.375 >>> curve1a.evaluate(s) == curve2.evaluate(t) array([[ True], [ True]]) >>> intersection = Intersection(0, s, 0, t) >>> edge_nodes1 = (nodes1a, None, None) >>> edge_nodes2 = (nodes2, None, None) >>> classify_intersection(intersection, edge_nodes1, edge_nodes2) Traceback (most recent call last): ... ValueError: ('Intersection occurs at the end of an edge', 's', 1.0, 't', 0.375) >>> >>> nodes1b = np.asfortranarray([ ... [9.0, 4.5, 0.0], ... [2.25, 2.375, 2.5], ... ]) >>> curve1b = bezier.Curve(nodes1b, degree=2) >>> curve1b.evaluate(0.0) == curve2.evaluate(t) array([[ True], [ True]]) >>> intersection = Intersection(1, 0.0, 0, t) >>> edge_nodes1 = (nodes1a, nodes1b, None) >>> classify_intersection(intersection, edge_nodes1, edge_nodes2) <IntersectionClassification.FIRST: 0>
As above, some intersections at the end of an edge are part of an actual intersection. However, some triangles may just “kiss” at a corner intersection:
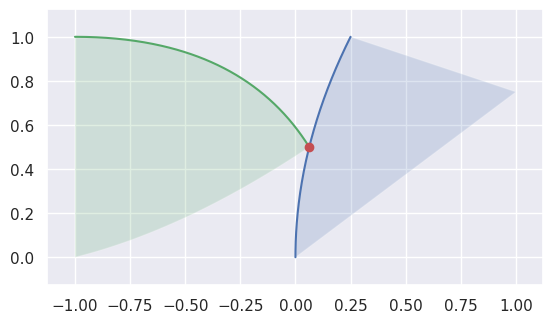
>>> nodes1 = np.asfortranarray([ ... [0.25, 0.0, 0.0, 0.625, 0.5 , 1.0 ], ... [1.0 , 0.5, 0.0, 0.875, 0.375, 0.75], ... ]) >>> triangle1 = bezier.Triangle(nodes1, degree=2) >>> nodes2 = np.asfortranarray([ ... [0.0625, -0.25, -1.0, -0.5 , -1.0, -1.0], ... [0.5 , 1.0 , 1.0, 0.125, 0.5, 0.0], ... ]) >>> triangle2 = bezier.Triangle(nodes2, degree=2) >>> curve1, _, _ = triangle1.edges >>> edge_nodes1 = [curve.nodes for curve in triangle1.edges] >>> curve2, _, _ = triangle2.edges >>> edge_nodes2 = [curve.nodes for curve in triangle2.edges] >>> s, t = 0.5, 0.0 >>> curve1.evaluate(s) == curve2.evaluate(t) array([[ True], [ True]]) >>> intersection = Intersection(0, s, 0, t) >>> classify_intersection(intersection, edge_nodes1, edge_nodes2) <IntersectionClassification.IGNORED_CORNER: 5>
Note
This assumes the intersection occurs in \(\mathbf{R}^2\) but doesn’t check this.
Note
This function doesn’t allow wiggle room / round-off when checking endpoints, nor when checking if the cross product is near zero, nor when curvatures are compared. However, the most “correct” version of this function likely should allow for some round off.
- Parameters:
intersection (Intersection) – An intersection object.
edge_nodes1 (
Tuplenumpy.ndarray,numpy.ndarray,numpy.ndarray) – The nodes of the three edges of the first triangle being intersected.edge_nodes2 (
Tuplenumpy.ndarray,numpy.ndarray,numpy.ndarray) – The nodes of the three edges of the second triangle being intersected.
- Returns:
The “inside” curve type, based on the classification enum.
- Return type:
- Raises:
ValueError – If the intersection occurs at the end of either curve involved. This is because we want to classify which curve to move forward on, and we can’t move past the end of a segment.
- bezier.hazmat.triangle_helpers.handle_ends(index1, s, index2, t)¶
Updates intersection parameters if it is on the end of an edge.
Note
This is a helper used only by
Triangle.intersect().Does nothing if the intersection happens in the middle of two edges.
If the intersection occurs at the end of the first curve, moves it to the beginning of the next edge. Similar for the second curve.
This function is used as a pre-processing step before passing an intersection to
classify_intersection(). There, only corners that begin an edge are considered, since that function is trying to determine which edge to move forward on.- Parameters:
- Returns:
A triple of:
flag indicating if the intersection is at the end of an edge
flag indicating if the intersection is a “corner”
4-tuple of the “updated” values
(index1, s, index2, t)
- Return type:
- bezier.hazmat.triangle_helpers.to_front(intersection, intersections, unused)¶
Rotates a node to the “front”.
Note
This is a helper used only by
basic_interior_combine(), which in turn is only used bycombine_intersections().If a node is at the end of a segment, moves it to the beginning of the next segment (at the exact same point). We assume that callers have pruned
intersectionsso that there are none withs == 1.0ort == 1.0. Hence, any such intersection will be an “artificial” intersection added byget_next().Note
This method checks for exact endpoints, i.e. parameter bitwise identical to
1.0. But it may make sense to allow some wiggle room.- Parameters:
intersection (Intersection) – The current intersection.
intersections (
ListIntersection) – List of all detected intersections, provided as a reference for of potential points to arrive at.unused (
ListIntersection) – List nodes that haven’t been used yet in an intersection curved polygon
- Returns:
An intersection to (maybe) move to the beginning of the next edge of the triangle.
- Return type:
- bezier.hazmat.triangle_helpers.get_next_first(intersection, intersections, to_end=True)¶
Gets the next node along the current (first) edge.
Note
This is a helper used only by
get_next(), which in turn is only used bybasic_interior_combine(), which itself is only used bycombine_intersections().Along with
get_next_second(), this function does the majority of the heavy lifting inget_next(). Very similar toget_next_second(), but this works with the first curve while the other function works with the second.- Parameters:
intersection (Intersection) – The current intersection.
intersections (
ListIntersection) – List of all detected intersections, provided as a reference for potential points to arrive at.to_end (
Optionalbool) – Indicates if the next node should just be the end of the first edge orNone.
- Returns:
point along a triangle of intersection. This will produce the next
OptionalIntersection: The “next” intersection along the current (first) edge or the end of the same edge. Ifto_endisFalseand there are no other intersections along the current edge, will returnNone(rather than the end of the same edge).
- bezier.hazmat.triangle_helpers.get_next_second(intersection, intersections, to_end=True)¶
Gets the next node along the current (second) edge.
Note
This is a helper used only by
get_next(), which in turn is only used bybasic_interior_combine(), which itself is only used bycombine_intersections().Along with
get_next_first(), this function does the majority of the heavy lifting inget_next(). Very similar toget_next_first(), but this works with the second curve while the other function works with the first.- Parameters:
intersection (Intersection) – The current intersection.
intersections (
ListIntersection) – List of all detected intersections, provided as a reference for potential points to arrive at.to_end (
Optionalbool) – Indicates if the next node should just be the end of the first edge orNone.
- Returns:
point along a triangle of intersection. This will produce the next
OptionalIntersection: The “next” intersection along the current (second) edge or the end of the same edge. Ifto_endisFalseand there are no other intersections along the current edge, will returnNone(rather than the end of the same edge).
- bezier.hazmat.triangle_helpers.get_next_coincident(intersection, intersections)¶
Gets the next node along the current (coincident) edge.
Note
This is a helper used only by
get_next(), which in turn is only used bybasic_interior_combine(), which itself is only used bycombine_intersections().Along with
get_next_first()andget_next_second(), this function does the majority of the heavy lifting inget_next().This function moves immediately to the “next” intersection along the “current” edge. An intersection labeled as
COINCIDENTcan only occur at the beginning of a segment. The end will correspond to thesortparameter being equal to1.0and so it will get “rotated” to the front of the next edge, where it will be classified according to a different edge pair.It’s also worth noting that some coincident segments will correspond to curves moving in opposite directions. In that case, there is no “interior” intersection (the curves are facing away) and so that segment won’t be part of an intersection.
- Parameters:
intersection (Intersection) – The current intersection.
intersections (
ListIntersection) – List of all detected intersections, provided as a reference for potential points to arrive at.
- Returns:
The “next” point along a triangle of intersection. This will produce the next intersection along the current (second) edge or the end of the same edge.
- Return type:
- bezier.hazmat.triangle_helpers.is_first(classification)¶
Check if a classification is on the “first” curve.
- Parameters:
classification (IntersectionClassification) – The classification being checked.
- Returns:
Indicating if the classification is on the first curve.
- Return type:
- bezier.hazmat.triangle_helpers.is_second(classification)¶
Check if a classification is on the “second” curve.
- Parameters:
classification (IntersectionClassification) – The classification being checked.
- Returns:
Indicating if the classification is on the second curve.
- Return type:
- bezier.hazmat.triangle_helpers.get_next(intersection, intersections, unused)¶
Gets the next node along a given edge.
Note
This is a helper used only by
basic_interior_combine(), which in turn is only used bycombine_intersections(). This function does the majority of the heavy lifting forbasic_interior_combine().Note
This function returns
Intersectionobjects even when the point isn’t strictly an intersection. This is “incorrect” in some sense, but for now, we don’t bother implementing a class similar to, but different from,Intersectionto satisfy this need.- Parameters:
intersection (Intersection) – The current intersection.
intersections (
ListIntersection) – List of all detected intersections, provided as a reference for of potential points to arrive at.unused (
ListIntersection) – List nodes that haven’t been used yet in an intersection curved polygon
- Returns:
The “next” point along a triangle of intersection. This will produce the next intersection along the current edge or the end of the current edge.
- Return type:
- Raises:
ValueError – If the intersection is not classified as
FIRST,TANGENT_FIRST,SECOND,TANGENT_SECONDorCOINCIDENT.
- bezier.hazmat.triangle_helpers.ends_to_curve(start_node, end_node)¶
Convert a “pair” of intersection nodes to a curve segment.
Note
This is a helper used only by
basic_interior_combine(), which in turn is only used bycombine_intersections().Note
This function could specialize to the first or second segment attached to
start_nodeandend_node. We determine first / second based on the classification ofstart_node, but the callers of this function could provide that information / isolate the base curve and the two parameters for us.Note
This only checks the classification of the
start_node.- Parameters:
start_node (Intersection) – The beginning of a segment.
end_node (Intersection) – The end of (the same) segment.
- Returns:
The 3-tuple of:
The edge index along the first triangle (if in
{0, 1, 2}) or the edge index along the second triangle shifted to the right by 3 (if in{3, 4, 5})The start parameter along the edge
The end parameter along the edge
- Return type:
- Raises:
ValueError – If the
start_nodeandend_nodedisagree on the first curve when classified asFIRST.ValueError – If the
start_nodeandend_nodedisagree on the second curve when classified asSECOND.ValueError – If the
start_nodeandend_nodedisagree on the both curves when classified asCOINCIDENT.ValueError – If the
start_nodeis not classified asFIRST,TANGENT_FIRST,SECOND,TANGENT_SECONDorCOINCIDENT.
- bezier.hazmat.triangle_helpers.no_intersections(nodes1, degree1, nodes2, degree2)¶
Determine if one triangle is in the other.
Helper for
combine_intersections()that handles the case of no points of intersection. In this case, either the triangles are disjoint or one is fully contained in the other.To check containment, it’s enough to check if one of the corners is contained in the other triangle.
- Parameters:
nodes1 (numpy.ndarray) – The nodes defining the first triangle in the intersection (assumed in :math:mathbf{R}^2`).
degree1 (int) – The degree of the triangle given by
nodes1.nodes2 (numpy.ndarray) – The nodes defining the second triangle in the intersection (assumed in :math:mathbf{R}^2`).
degree2 (int) – The degree of the triangle given by
nodes2.
- Returns:
Pair (2-tuple) of
- Return type:
- bezier.hazmat.triangle_helpers.tangent_only_intersections(all_types)¶
Determine intersection in the case of only-tangent intersections.
If the only intersections are tangencies, then either the triangles are tangent but don’t meet (“kissing” edges) or one triangle is internally tangent to the other.
Thus we expect every intersection to be classified as
TANGENT_FIRST,TANGENT_SECOND,OPPOSED,IGNORED_CORNERorCOINCIDENT_UNUSED.What’s more, we expect all intersections to be classified the same for a given pairing.
- Parameters:
all_types (
SetIntersectionClassification) – The set of all intersection classifications encountered among the intersections for the given triangle-triangle pair.- Returns:
Pair (2-tuple) of
- Return type:
- Raises:
ValueError – If there are intersections of more than one type among
TANGENT_FIRST,TANGENT_SECOND,OPPOSED,IGNORED_CORNERorCOINCIDENT_UNUSED.ValueError – If there is a unique classification, but it isn’t one of the tangent types.
- bezier.hazmat.triangle_helpers.basic_interior_combine(intersections, max_edges=10)¶
Combine intersections that don’t involve tangencies.
Note
This is a helper used only by
combine_intersections().Note
This helper assumes
intersectionsisn’t empty, but doesn’t enforce it.- Parameters:
intersections (
ListIntersection) – Intersections from each of the 9 edge-edge pairs from a triangle-triangle pairing.max_edges (
Optionalint) – The maximum number of allowed / expected edges per intersection. This is to avoid infinite loops.
- Returns:
Pair (2-tuple) of
List of “edge info” lists. Each list represents a curved polygon and contains 3-tuples of edge index, start and end (see the output of
ends_to_curve()).”Contained” boolean. If not
None, indicates that one of the triangles is contained in the other.
- Return type:
- Raises:
RuntimeError – If the number of edges in a curved polygon exceeds
max_edges. This is interpreted as a sign that the algorithm failed.
- bezier.hazmat.triangle_helpers.combine_intersections(intersections, nodes1, degree1, nodes2, degree2, all_types)¶
Combine curve-curve intersections into curved polygon(s).
Note
This is a helper used only by
Triangle.intersect().Does so assuming each intersection lies on an edge of one of two
Triangle-s.Note
This assumes that each
intersectionhas been classified viaclassify_intersection()and only the intersections classified asFIRSTandSECONDwere kept.- Parameters:
intersections (
ListIntersection) – Intersections from each of the 9 edge-edge pairs from a triangle-triangle pairing.nodes1 (numpy.ndarray) – The nodes defining the first triangle in the intersection (assumed in \(\mathbf{R}^2\)).
degree1 (int) – The degree of the triangle given by
nodes1.nodes2 (numpy.ndarray) – The nodes defining the second triangle in the intersection (assumed in \(\mathbf{R}^2\)).
degree2 (int) – The degree of the triangle given by
nodes2.all_types (
SetIntersectionClassification) – The set of all intersection classifications encountered among the intersections for the given triangle-triangle pair.
- Returns:
Pair (2-tuple) of
List of “edge info” lists. Each list represents a curved polygon and contains 3-tuples of edge index, start and end (see the output of
ends_to_curve()).”Contained” boolean. If not
None, indicates that one of the triangles is contained in the other.
- Return type:
- bezier.hazmat.triangle_helpers.evaluate_barycentric(nodes, degree, lambda1, lambda2, lambda3)¶
Compute a point on a triangle.
Evaluates \(B\left(\lambda_1, \lambda_2, \lambda_3\right)\) for a Bézier triangle / triangle defined by
nodes.Note
There is also a Fortran implementation of this function, which will be used if it can be built.
- Parameters:
nodes (numpy.ndarray) – Control point nodes that define the triangle.
degree (int) – The degree of the triangle define by
nodes.lambda1 (float) – Parameter along the reference triangle.
lambda2 (float) – Parameter along the reference triangle.
lambda3 (float) – Parameter along the reference triangle.
- Returns:
The evaluated point as a
D x 1array (whereDis the ambient dimension wherenodesreside).- Return type:
- bezier.hazmat.triangle_helpers.evaluate_barycentric_multi(nodes, degree, param_vals, dimension)¶
Compute multiple points on the triangle.
Note
There is also a Fortran implementation of this function, which will be used if it can be built.
- Parameters:
nodes (numpy.ndarray) – Control point nodes that define the triangle.
degree (int) – The degree of the triangle define by
nodes.param_vals (numpy.ndarray) – Array of parameter values (as a
N x 3array).dimension (int) – The dimension the triangle lives in.
- Returns:
The evaluated points, where columns correspond to rows of
param_valsand the rows to the dimension of the underlying triangle.- Return type:
- bezier.hazmat.triangle_helpers.evaluate_cartesian_multi(nodes, degree, param_vals, dimension)¶
Compute multiple points on the triangle.
Note
There is also a Fortran implementation of this function, which will be used if it can be built.
- Parameters:
nodes (numpy.ndarray) – Control point nodes that define the triangle.
degree (int) – The degree of the triangle define by
nodes.param_vals (numpy.ndarray) – Array of parameter values (as a
N x 2array).dimension (int) – The dimension the triangle lives in.
- Returns:
The evaluated points, where columns correspond to rows of
param_valsand the rows to the dimension of the underlying triangle.- Return type:
- bezier.hazmat.triangle_helpers.compute_edge_nodes(nodes, degree)¶
Compute the nodes of each edges of a triangle.
Note
There is also a Fortran implementation of this function, which will be used if it can be built.
- Parameters:
nodes (numpy.ndarray) – Control point nodes that define the triangle.
degree (int) – The degree of the triangle define by
nodes.
- Returns:
The nodes in the edges of the triangle.
- Return type:
- bezier.hazmat.triangle_helpers.shoelace_for_area(nodes)¶
Compute an auxiliary “shoelace” sum used to compute area.
Note
This is a helper for
compute_area().Defining \(\left[i, j\right] = x_i y_j - y_i x_j\) as a shoelace term illuminates the name of this helper. On a degree one curve, this function will return
\[\frac{1}{2}\left[0, 1\right].\]on a degree two curve it will return
\[\frac{1}{6}\left(2 \left[0, 1\right] + 2 \left[1, 2\right] + \left[0, 2\right]\right)\]and so on.
For a given \(\left[i, j\right]\), the coefficient comes from integrating \(b_{i, d}, b_{j, d}\) on \(\left[0, 1\right]\) (where \(b_{i, d}, b_{j, d}\) are Bernstein basis polynomials).
- Returns:
The computed sum of shoelace terms.
- Return type:
- Raises:
UnsupportedDegree – If the degree is not 1, 2, 3 or 4.
- bezier.hazmat.triangle_helpers.compute_area(edges)¶
Compute the area of a curved polygon.
Note
There is also a Fortran implementation of this function, which will be used if it can be built.
Uses Green’s theorem to compute the area exactly. See
Triangle.areaandCurvedPolygon.areafor more information.- Parameters:
edges (
Tuplenumpy.ndarray) – A list of2 x Narrays, each of which are control points for an edge of a curved polygon.- Returns:
The computed area.
- Return type: