bezier.surface module¶

Helper for Bézier Surfaces / Triangles.

class bezier.surface.Surface(nodes, base_x=0.0, base_y=0.0, width=1.0, _copy=True)¶

Bases: bezier._base.Base

Represents a Bézier surface.

We define a Bézier triangle as a mapping from the unit simplex in 2D (i.e. the unit triangle) onto a surface in an arbitrary dimension. We use barycentric coordinates

\[\lambda_1 = 1 - s - t, \lambda_2 = s, \lambda_3 = t\]

for points in

\[\left\{(s, t) \mid 0 \leq s, t, s + t \leq 1\right\}.\]

As with curves, using these weights we get convex combinations of points \(v_{i, j, k}\) in some vector space:

\[B\left(\lambda_1, \lambda_2, \lambda_3\right) = \sum_{i + j + k = d} \binom{d}{i \, j \, k} \lambda_1^i \lambda_2^j \lambda_3^k \cdot v_{i, j, k}\]

Note

We assume the nodes are ordered from left-to-right and from bottom-to-top. So for example, the linear triangle:

(0,0,1)

(1,0,0)  (0,1,0)

is ordered as

\[\begin{split}\left[\begin{array}{c c c} v_{1,0,0} & v_{0,1,0} & v_{0,0,1} \end{array}\right]^T\end{split}\]

the quadratic triangle:

(0,0,2)

(1,0,1)  (0,1,1)

(2,0,0)  (1,1,0)  (0,2,0)

is ordered as

\[\begin{split}\left[\begin{array}{c c c c c c} v_{2,0,0} & v_{1,1,0} & v_{0,2,0} & v_{1,0,1} & v_{0,1,1} & v_{0,0,2} \end{array}\right]^T\end{split}\]

the cubic triangle:

(0,0,3)

(1,0,2)  (0,1,2)

(2,0,1)  (1,1,1)  (0,2,1)

(3,0,0)  (2,1,0)  (1,2,0)  (0,3,0)

is ordered as

\[\begin{split}\left[\begin{array}{c c c c c c c c c c} v_{3,0,0} & v_{2,1,0} & v_{1,2,0} & v_{0,3,0} & v_{2,0,1} & v_{1,1,1} & v_{0,2,1} & v_{1,0,2} & v_{0,1,2} & v_{0,0,3} \end{array}\right]^T\end{split}\]

and so on.

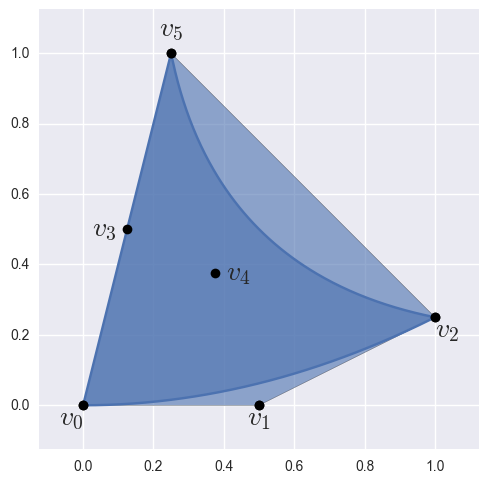
>>> import bezier
>>> nodes = np.array([
...     [0.0  , 0.0  ],
...     [0.5  , 0.0  ],
...     [1.0  , 0.25 ],
...     [0.125, 0.5  ],
...     [0.375, 0.375],
...     [0.25 , 1.0  ],
... ])
>>> surface = bezier.Surface(nodes)
>>> surface
<Surface (degree=2, dimension=2)>

Parameters:

nodes (numpy.ndarray) – The nodes in the surface. The rows represent each node while the columns are the dimension of the ambient space.
base_x (Optional [ float ]) – The \(x\)-coordinate of the base vertex of the sub-triangle that this surface represents.
base_y (Optional [ float ]) – The \(y\)-coordinate of the base vertex of the sub-triangle that this surface represents.
width (Optional [ float ]) – The width of the sub-triangle that this surface represents.
_copy (bool) – Flag indicating if the nodes should be copied before being stored. Defaults to True since callers may freely mutate nodes after passing in.

__repr__()¶

Representation of current object.

Returns:	Object representation.
Return type:	str

area¶

float: The area of the current surface.

Raises:	`NotImplementedError` – If the area isn’t already cached.

width¶

float: The “width” of the parameterized triangle.

When re-parameterizing (e.g. via subdivide()) we specialize the surface from the unit triangle to some sub-triangle. After doing this, we re-parameterize so that that sub-triangle is treated like the unit triangle.

To track which sub-triangle we are in during the subdivision process, we use the coordinates of the base vertex as well as the “width” of each leg.

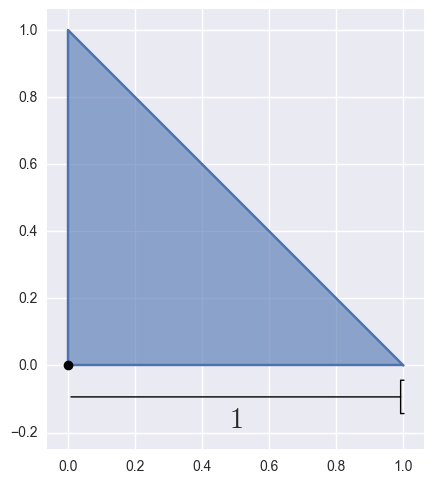
>>> surface.base_x, surface.base_y
(0.0, 0.0)
>>> surface.width
1.0

Upon subdivision, the width halves (and potentially changes sign) and the vertex moves to one of four points:

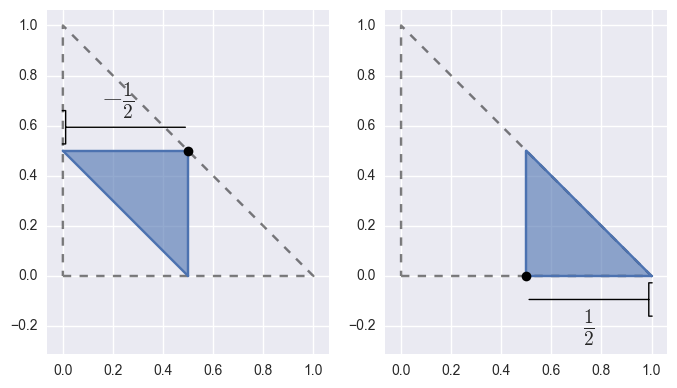
>>> _, sub_surface_b, sub_surface_c, _ = surface.subdivide()
>>> sub_surface_b.base_x, sub_surface_b.base_y
(0.5, 0.5)
>>> sub_surface_b.width
-0.5
>>> sub_surface_c.base_x, sub_surface_c.base_y
(0.5, 0.0)
>>> sub_surface_c.width
0.5

base_x¶

float: The x-coordinate of the base vertex.

See width() for more detail.

base_y¶

float: The y-coordinate of the base vertex.

See width() for more detail.

edges¶

tuple: The edges of the surface.

>>> nodes = np.array([
...     [0.0   ,  0.0   ],
...     [0.5   , -0.1875],
...     [1.0   ,  0.0   ],
...     [0.1875,  0.5   ],
...     [0.625 ,  0.625 ],
...     [0.0   ,  1.0   ],
... ])
>>> surface = bezier.Surface(nodes)
>>> edge1, _, _ = surface.edges
>>> edge1
<Curve (degree=2, dimension=2)>
>>> edge1.nodes
array([[ 0.  ,  0.    ],
       [ 0.5 , -0.1875],
       [ 1.  ,  0.    ]])

Returns:	The edges of the surface.
Return type:	`Tuple` [ `Curve`, `Curve`, `Curve` ]

evaluate_barycentric(lambda1, lambda2, lambda3)¶

Compute a point on the surface.

Evaluates \(B\left(\lambda_1, \lambda_2, \lambda_3\right)\).

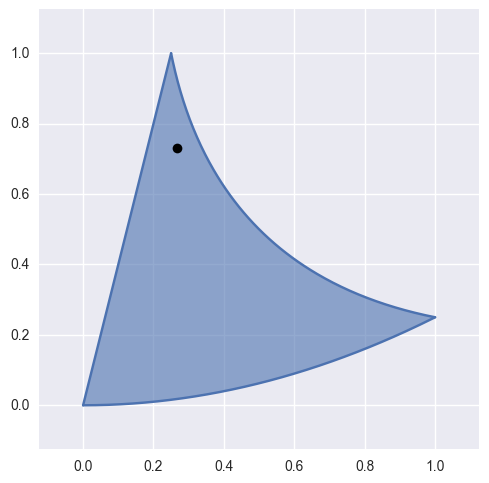
../_images/surface_evaluate_barycentric.png

>>> nodes = np.array([
...     [0.0  , 0.0  ],
...     [0.5  , 0.0  ],
...     [1.0  , 0.25 ],
...     [0.125, 0.5  ],
...     [0.375, 0.375],
...     [0.25 , 1.0  ],
... ])
>>> surface = bezier.Surface(nodes)
>>> point = surface.evaluate_barycentric(0.125, 0.125, 0.75)
>>> point
array([ 0.265625 , 0.73046875])

However, this can’t be used for points outside the reference triangle:

>>> surface.evaluate_barycentric(-0.25, 0.75, 0.5)
Traceback (most recent call last):
  ...
ValueError: ('Parameters must be positive', -0.25, 0.75, 0.5)

or for non-Barycentric coordinates;

>>> surface.evaluate_barycentric(0.25, 0.25, 0.25)
Traceback (most recent call last):
  ...
ValueError: ('Values do not sum to 1', 0.25, 0.25, 0.25)

Parameters:	lambda1 (float) – Parameter along the reference triangle. lambda2 (float) – Parameter along the reference triangle. lambda3 (float) – Parameter along the reference triangle.
Returns:	The point on the surface (as a one dimensional NumPy array).
Return type:	numpy.ndarray
Raises:	`ValueError` – If the weights are not valid barycentric coordinates, i.e. they don’t sum to `1`. `ValueError` – If some weights are negative.

evaluate_cartesian(s, t)¶

Compute a point on the surface.

Evaluates \(B\left(1 - s - t, s, t\right)\) by calling evaluate_barycentric().

Parameters:	s (float) – Parameter along the reference triangle. t (float) – Parameter along the reference triangle.
Returns:	The point on the surface (as a one dimensional NumPy array).
Return type:	numpy.ndarray

evaluate_multi(param_vals)¶

Compute multiple points on the surface.

If param_vals has two columns, this method treats them as Cartesian: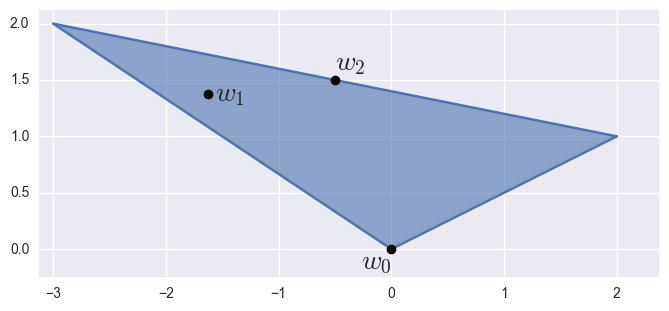

>>> nodes = np.array([
...     [ 0.0, 0.0],
...     [ 2.0, 1.0],
...     [-3.0, 2.0],
... ])
>>> surface = bezier.Surface(nodes)
>>> surface
<Surface (degree=1, dimension=2)>
>>> param_vals = np.array([
...     [0.0  , 0.0  ],
...     [0.125, 0.625],
...     [0.5  , 0.5  ],
... ])
>>> points = surface.evaluate_multi(param_vals)
>>> points
array([[ 0.   , 0.   ],
       [-1.625, 1.375],
       [-0.5  , 1.5  ]])

and if param_vals has three columns, treats them as Barycentric: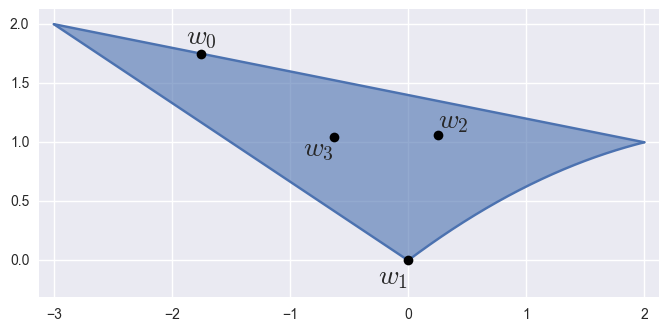

>>> nodes = np.array([
...     [ 0. , 0.  ],
...     [ 1. , 0.75],
...     [ 2. , 1.  ],
...     [-1.5, 1.  ],
...     [-0.5, 1.5 ],
...     [-3. , 2.  ],
... ])
>>> surface = bezier.Surface(nodes)
>>> surface
<Surface (degree=2, dimension=2)>
>>> param_vals = np.array([
...     [0.   , 0.25, 0.75 ],
...     [1.   , 0.  , 0.   ],
...     [0.25 , 0.5 , 0.25 ],
...     [0.375, 0.25, 0.375],
... ])
>>> points = surface.evaluate_multi(param_vals)
>>> points
array([[-1.75  , 1.75    ],
       [ 0.    , 0.      ],
       [ 0.25  , 1.0625  ],
       [-0.625 , 1.046875]])

Note

This currently just uses evaluate_cartesian() and evaluate_barycentric() so is less performant than it could be.

Parameters:	param_vals (numpy.ndarray) – Array of parameter values (as a 2D array).
Returns:	The point on the surface.
Return type:	numpy.ndarray
Raises:	`ValueError` – If `param_vals` is not a 2D array. `ValueError` – If `param_vals` doesn’t have 2 or 3 columns.

plot(pts_per_edge, ax=None, with_nodes=False, show=False)¶

Plot the current surface.

Parameters:	pts_per_edge (int) – Number of points to plot per edge. ax (`Optional` [ `matplotlib.artist.Artist` ]) – matplotlib axis object to add plot to. with_nodes (`Optional` [ `bool` ]) – Determines if the control points should be added to the plot. Off by default. show (`Optional` [ `bool` ]) – Flag indicating if the plot should be shown.
Returns:	The axis containing the plot. This may be a newly created axis.
Return type:	matplotlib.artist.Artist
Raises:	`NotImplementedError` – If the surface’s dimension is not `2`.

subdivide()¶

Split the surface into four sub-surfaces.

Does so by taking the unit triangle (i.e. the domain of the surface) and splitting it into four sub-triangles

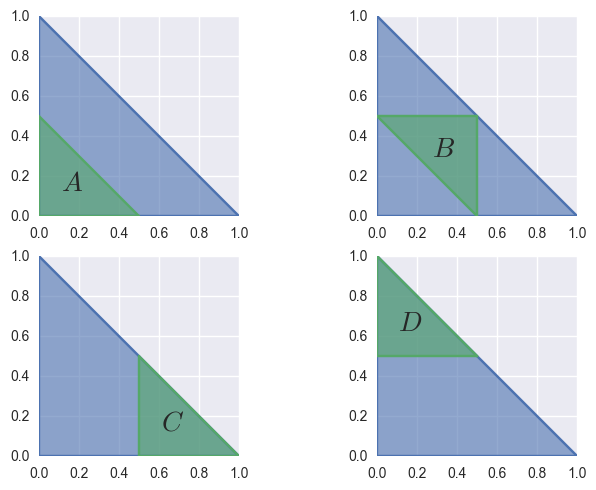
Then the surface is re-parameterized via the map to/from the given sub-triangles and the unit triangle.

For example, when a degree two surface is subdivided:

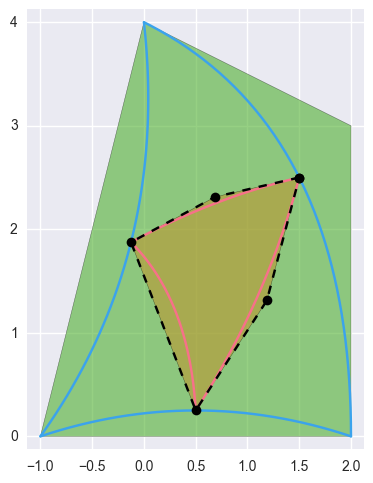
>>> nodes = np.array([
...     [-1.0 , 0.0 ],
...     [ 0.5 , 0.5 ],
...     [ 2.0 , 0.0 ],
...     [ 0.25, 1.75],
...     [ 2.0 , 3.0 ],
...     [ 0.0 , 4.0 ],
... ])
>>> surface = bezier.Surface(nodes)
>>> _, sub_surface_b, _, _ = surface.subdivide()
>>> sub_surface_b
<Surface (degree=2, dimension=2, base=(0.5, 0.5), width=-0.5)>
>>> sub_surface_b.nodes
array([[ 1.5   , 2.5   ],
       [ 0.6875, 2.3125],
       [-0.125 , 1.875 ],
       [ 1.1875, 1.3125],
       [ 0.4375, 1.3125],
       [ 0.5   , 0.25  ]])

Returns:	The lower left, central, lower right and upper left sub-surfaces (in that order).
Return type:	`Tuple` [ `Surface`, `Surface`, `Surface`, `Surface` ]

is_valid¶

bool: Flag indicating if the surface is “valid”.

Here, “valid” means there are no self-intersections or singularities.

This checks if the Jacobian of the map from the reference triangle is nonzero. For example, a linear “surface” with collinear points is invalid:

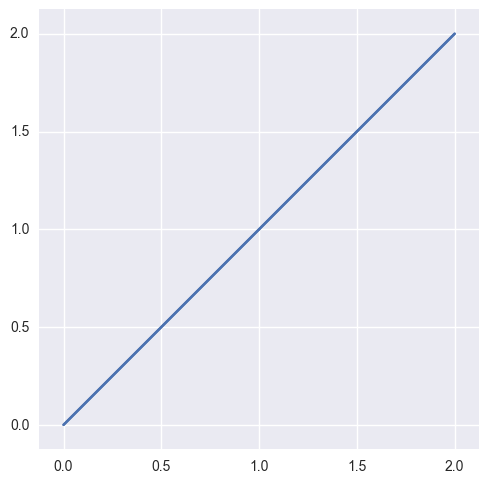
>>> nodes = np.array([
...     [0.0, 0.0],
...     [1.0, 1.0],
...     [2.0, 2.0],
... ])
>>> surface = bezier.Surface(nodes)
>>> surface.is_valid
False

while a quadratic surface with one straight side:

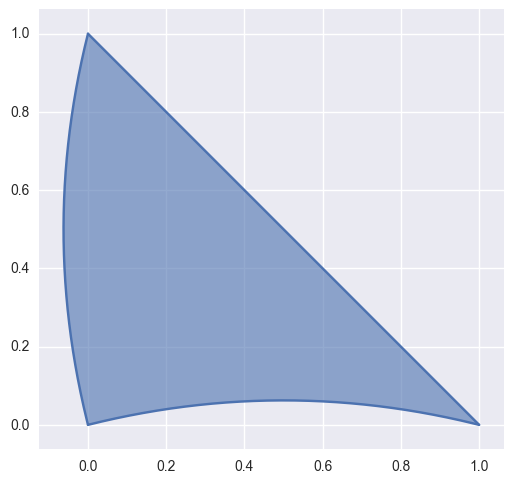
>>> nodes = np.array([
...     [ 0.0  , 0.0  ],
...     [ 0.5  , 0.125],
...     [ 1.0  , 0.0  ],
...     [-0.125, 0.5  ],
...     [ 0.5  , 0.5  ],
...     [ 0.0  , 1.0  ],
... ])
>>> surface = bezier.Surface(nodes)
>>> surface.is_valid
True

though not all higher degree surfaces are valid:

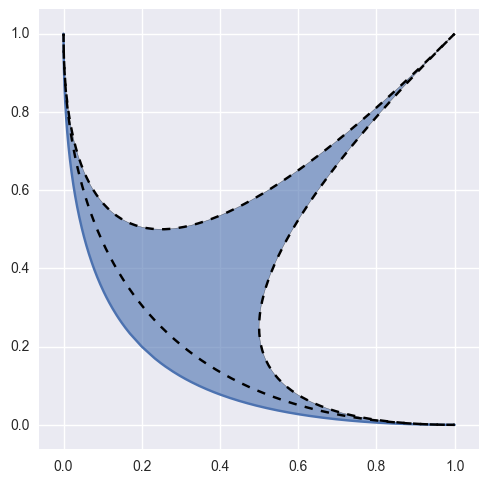
>>> nodes = np.array([
...     [1.0, 0.0],
...     [0.0, 0.0],
...     [1.0, 1.0],
...     [0.0, 0.0],
...     [0.0, 0.0],
...     [0.0, 1.0],
... ])
>>> surface = bezier.Surface(nodes)
>>> surface.is_valid
False

locate(point)¶

Find a point on the current surface.

Solves for \(s\) and \(t\) in \(B(s, t) = p\).

Note

A unique solution is only guaranteed if the current surface is valid. This code assumes a valid surface, but doesn’t check.

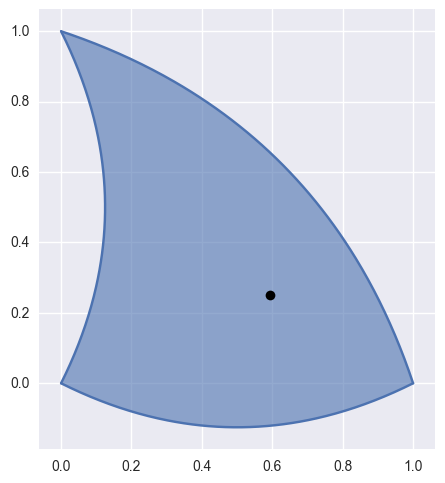
>>> surface = bezier.Surface(np.array([
...     [0.0 ,  0.0 ],
...     [0.5 , -0.25],
...     [1.0 ,  0.0 ],
...     [0.25,  0.5 ],
...     [0.75,  0.75],
...     [0.0 ,  1.0 ],
... ]))
>>> point = np.array([[0.59375, 0.25]])
>>> s, t = surface.locate(point)
>>> s
0.5
>>> t
0.25

Parameters:	point (numpy.ndarray) – A (`1xD`) point on the surface, where \(D\) is the dimension of the surface.
Returns:	The \(s\) and \(t\) values corresponding to `x_val` and `y_val` or `None` if the point is not on the `surface`.
Return type:	`Optional` [ `Tuple` [ `float`, `float` ] ]
Raises:	`NotImplementedError` – If the surface isn’t in \(\mathbf{R}^2\). `ValueError` – If the dimension of the `point` doesn’t match the dimension of the current surface.

intersect(other)¶

Find the common intersection with another surface.

Parameters:	other (Surface) – Other surface to intersect with.
Returns:	List of intersection objects (possibly empty).
Return type:	list
Raises:	`TypeError` – If `other` is not a surface. `NotImplementedError` – If both surfaces aren’t two-dimensional.

__eq__(other)¶

Check equality against another shape.

Returns:	Boolean indicating if the shapes are the same.
Return type:	bool

__ne__(other)¶

Check inequality against another shape.

Returns:	Boolean indicating if the shapes are not the same.
Return type:	bool

copy()¶

Make a copy of the current shape.

Returns:	Instance of the current shape.

degree¶: int: The degree of the current shape.

dimension¶

int: The dimension that the shape lives in.

For example, if the shape lives in \(\mathbf{R}^3\), then the dimension is 3.

nodes¶: numpy.ndarray: The nodes that define the current shape.