bezier.curved_polygon module¶
Curved polygon and associated helpers.
A curved polygon (in \(\mathbf{R}^2\)) is defined by the collection of Bézier curves that determine the boundary.
-
class
bezier.curved_polygon.CurvedPolygon(*edges, **kwargs)¶ Bases:
objectRepresents an object defined by its curved boundary.
The boundary is a piecewise defined collection of Bézier curves.
Note
The direction of the nodes in each
Curveon the boundary is important. When verifying, we check that one curve begins where the last one ended.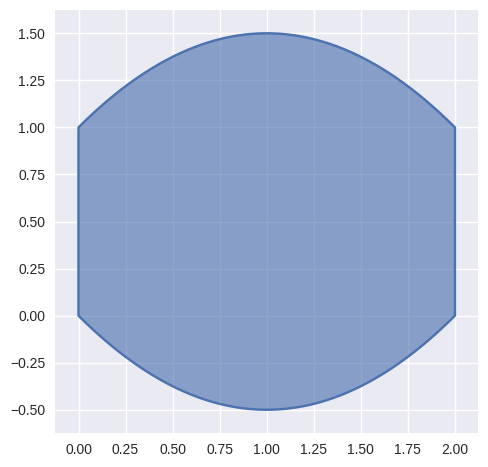
>>> import bezier >>> nodes0 = np.asfortranarray([ ... [0.0, 0.0], ... [1.0, -1.0], ... [2.0, 0.0], ... ]) >>> edge0 = bezier.Curve(nodes0, degree=2) >>> nodes1 = np.asfortranarray([ ... [2.0, 0.0], ... [2.0, 1.0], ... ]) >>> edge1 = bezier.Curve(nodes1, degree=1) >>> nodes2 = np.asfortranarray([ ... [2.0, 1.0], ... [1.0, 2.0], ... [0.0, 1.0], ... ]) >>> edge2 = bezier.Curve(nodes2, degree=2) >>> nodes3 = np.asfortranarray([ ... [0.0, 1.0], ... [0.0, 0.0], ... ]) >>> edge3 = bezier.Curve(nodes3, degree=1) >>> curved_poly = bezier.CurvedPolygon( ... edge0, edge1, edge2, edge3) >>> curved_poly <CurvedPolygon (num_sides=4)>
Though the endpoints of each pair of edges are verified to match, the curved polygon as a whole is not verified, so creating a curved polygon with self-intersections is possible:
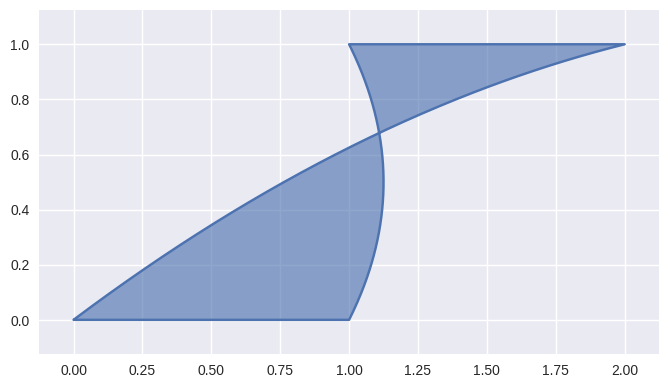
>>> nodes0 = np.asfortranarray([ ... [0.0, 0.0], ... [1.0, 0.0], ... ]) >>> edge0 = bezier.Curve(nodes0, degree=1) >>> nodes1 = np.asfortranarray([ ... [1.0 , 0.0], ... [1.25, 0.5], ... [1.0 , 1.0], ... ]) >>> edge1 = bezier.Curve(nodes1, degree=2) >>> nodes2 = np.asfortranarray([ ... [1.0, 1.0], ... [2.0, 1.0], ... ]) >>> edge2 = bezier.Curve(nodes2, degree=1) >>> nodes3 = np.asfortranarray([ ... [2.0, 1.0 ], ... [1.0, 0.75], ... [0.0, 0.0 ], ... ]) >>> edge3 = bezier.Curve(nodes3, degree=2) >>> curved_poly = bezier.CurvedPolygon( ... edge0, edge1, edge2, edge3) >>> curved_poly <CurvedPolygon (num_sides=4)>
Parameters: - edges (
Tuple[Curve, … ]) – The boundary edges of the curved polygon. - kwargs –
There are two keyword arguments accepted:
metadata(Sequence): A sequence of triples associated with this curved polygon. This is intended to be used by callers that have created a curved polygon as an intersection between two Bézier surfaces._verify(bool): Indicates if the edges should be verified as having shared endpoints. Defaults toTrue.
Other keyword arguments specified will be silently ignored.
-
num_sides¶ int – The number of sides in the current polygon.
-
plot(pts_per_edge, color=None, ax=None)¶ Plot the current curved polygon.
Parameters: Returns: The axis containing the plot. This may be a newly created axis.
Return type:
- edges (