bezier.surface module¶

Helper for Bézier Surfaces / Triangles.

class bezier.surface.Surface(nodes, degree, base_x=0.0, base_y=0.0, width=1.0, _copy=True)¶

Bases: bezier._base.Base

Represents a Bézier surface.

We define a Bézier triangle as a mapping from the unit simplex in 2D (i.e. the unit triangle) onto a surface in an arbitrary dimension. We use barycentric coordinates

\[\lambda_1 = 1 - s - t, \lambda_2 = s, \lambda_3 = t\]

for points in

\[\left\{(s, t) \mid 0 \leq s, t, s + t \leq 1\right\}.\]

As with curves, using these weights we get convex combinations of points \(v_{i, j, k}\) in some vector space:

\[B\left(\lambda_1, \lambda_2, \lambda_3\right) = \sum_{i + j + k = d} \binom{d}{i \, j \, k} \lambda_1^i \lambda_2^j \lambda_3^k \cdot v_{i, j, k}\]

Note

We assume the nodes are ordered from left-to-right and from bottom-to-top. So for example, the linear triangle:

(0,0,1)

(1,0,0)  (0,1,0)

is ordered as

\[\begin{split}\left[\begin{array}{c c c} v_{1,0,0} & v_{0,1,0} & v_{0,0,1} \end{array}\right]^T\end{split}\]

the quadratic triangle:

(0,0,2)

(1,0,1)  (0,1,1)

(2,0,0)  (1,1,0)  (0,2,0)

is ordered as

\[\begin{split}\left[\begin{array}{c c c c c c} v_{2,0,0} & v_{1,1,0} & v_{0,2,0} & v_{1,0,1} & v_{0,1,1} & v_{0,0,2} \end{array}\right]^T\end{split}\]

the cubic triangle:

(0,0,3)

(1,0,2)  (0,1,2)

(2,0,1)  (1,1,1)  (0,2,1)

(3,0,0)  (2,1,0)  (1,2,0)  (0,3,0)

is ordered as

\[\begin{split}\left[\begin{array}{c c c c c c c c c c} v_{3,0,0} & v_{2,1,0} & v_{1,2,0} & v_{0,3,0} & v_{2,0,1} & v_{1,1,1} & v_{0,2,1} & v_{1,0,2} & v_{0,1,2} & v_{0,0,3} \end{array}\right]^T\end{split}\]

and so on.

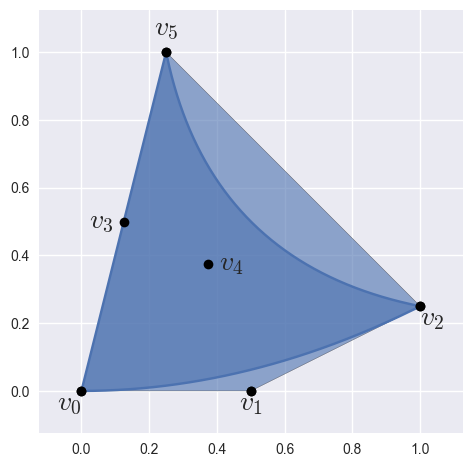
>>> import bezier
>>> nodes = np.array([
...     [0.0  , 0.0  ],
...     [0.5  , 0.0  ],
...     [1.0  , 0.25 ],
...     [0.125, 0.5  ],
...     [0.375, 0.375],
...     [0.25 , 1.0  ],
... ])
>>> surface = bezier.Surface(nodes, degree=2)
>>> surface
<Surface (degree=2, dimension=2)>

Parameters:

nodes (numpy.ndarray) – The nodes in the surface. The rows represent each node while the columns are the dimension of the ambient space.
degree (int) – The degree of the surface. This is assumed to correctly correspond to the number of nodes. Use from_nodes() if the degree has not yet been computed.
base_x (Optional [ float ]) – The \(x\)-coordinate of the base vertex of the sub-triangle that this surface represents.
base_y (Optional [ float ]) – The \(y\)-coordinate of the base vertex of the sub-triangle that this surface represents.
width (Optional [ float ]) – The width of the sub-triangle that this surface represents.
_copy (bool) – Flag indicating if the nodes should be copied before being stored. Defaults to True since callers may freely mutate nodes after passing in.

classmethod from_nodes(nodes, base_x=0.0, base_y=0.0, width=1.0, _copy=True)¶

Create a Surface from nodes.

Computes the degree based on the shape of nodes.

Parameters:	nodes (numpy.ndarray) – The nodes in the surface. The rows represent each node while the columns are the dimension of the ambient space. base_x (`Optional` [ `float` ]) – The \(x\)-coordinate of the base vertex of the sub-triangle that this surface represents. base_y (`Optional` [ `float` ]) – The \(y\)-coordinate of the base vertex of the sub-triangle that this surface represents. width (`Optional` [ `float` ]) – The width of the sub-triangle that this surface represents. _copy (bool) – Flag indicating if the nodes should be copied before being stored. Defaults to `True` since callers may freely mutate `nodes` after passing in.
Returns:	The constructed surface.
Return type:	Surface

__repr__()¶

Representation of current object.

Returns:	Object representation.
Return type:	str

area¶

float: The area of the current surface.

Raises:	`NotImplementedError` – If the area isn’t already cached.

width¶

float: The “width” of the parameterized triangle.

When re-parameterizing (e.g. via subdivide()) we specialize the surface from the unit triangle to some sub-triangle. After doing this, we re-parameterize so that that sub-triangle is treated like the unit triangle.

To track which sub-triangle we are in during the subdivision process, we use the coordinates of the base vertex as well as the “width” of each leg.

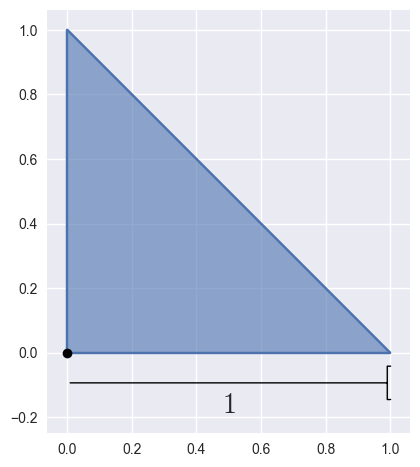
>>> surface.base_x, surface.base_y
(0.0, 0.0)
>>> surface.width
1.0

Upon subdivision, the width halves (and potentially changes sign) and the vertex moves to one of four points:

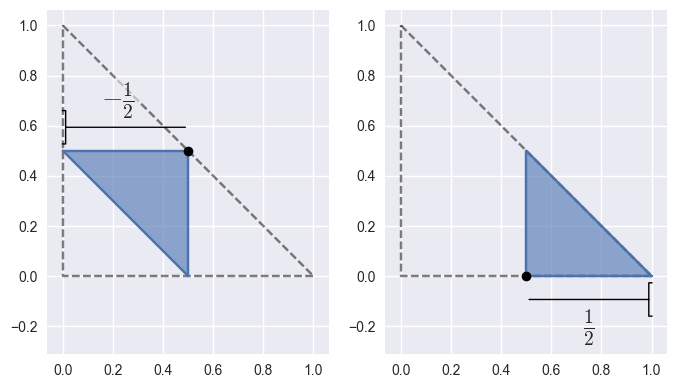
>>> _, sub_surface_b, sub_surface_c, _ = surface.subdivide()
>>> sub_surface_b.base_x, sub_surface_b.base_y
(0.5, 0.5)
>>> sub_surface_b.width
-0.5
>>> sub_surface_c.base_x, sub_surface_c.base_y
(0.5, 0.0)
>>> sub_surface_c.width
0.5

base_x¶

float: The x-coordinate of the base vertex.

See width() for more detail.

base_y¶

float: The y-coordinate of the base vertex.

See width() for more detail.

edges¶

tuple: The edges of the surface.

>>> nodes = np.array([
...     [0.0   ,  0.0   ],
...     [0.5   , -0.1875],
...     [1.0   ,  0.0   ],
...     [0.1875,  0.5   ],
...     [0.625 ,  0.625 ],
...     [0.0   ,  1.0   ],
... ])
>>> surface = bezier.Surface(nodes, 2)
>>> edge1, _, _ = surface.edges
>>> edge1
<Curve (degree=2, dimension=2)>
>>> edge1.nodes
array([[ 0.  ,  0.    ],
       [ 0.5 , -0.1875],
       [ 1.  ,  0.    ]])

Returns:	The edges of the surface.
Return type:	`Tuple` [ `Curve`, `Curve`, `Curve` ]

evaluate_barycentric(lambda1, lambda2, lambda3, _verify=True)¶

Compute a point on the surface.

Evaluates \(B\left(\lambda_1, \lambda_2, \lambda_3\right)\).

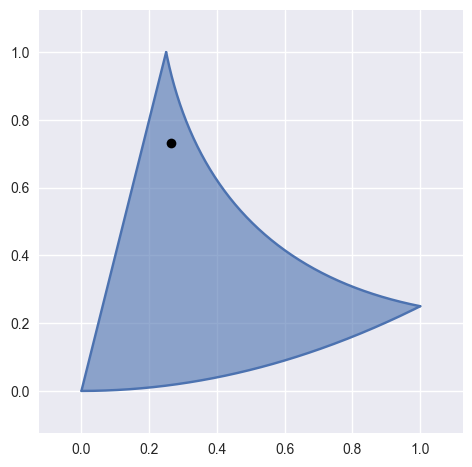
../_images/surface_evaluate_barycentric.png

>>> nodes = np.array([
...     [0.0  , 0.0  ],
...     [0.5  , 0.0  ],
...     [1.0  , 0.25 ],
...     [0.125, 0.5  ],
...     [0.375, 0.375],
...     [0.25 , 1.0  ],
... ])
>>> surface = bezier.Surface(nodes, 2)
>>> point = surface.evaluate_barycentric(0.125, 0.125, 0.75)
>>> point
array([[ 0.265625 , 0.73046875]])

However, this can’t be used for points outside the reference triangle:

>>> surface.evaluate_barycentric(-0.25, 0.75, 0.5)
Traceback (most recent call last):
  ...
ValueError: ('Parameters must be positive', -0.25, 0.75, 0.5)

or for non-Barycentric coordinates;

>>> surface.evaluate_barycentric(0.25, 0.25, 0.25)
Traceback (most recent call last):
  ...
ValueError: ('Values do not sum to 1', 0.25, 0.25, 0.25)

However, these “invalid” inputs can be used if _verify is False.

>>> surface.evaluate_barycentric(-0.25, 0.75, 0.5, _verify=False)
array([[ 0.6875 , 0.546875]])
>>> surface.evaluate_barycentric(0.25, 0.25, 0.25, _verify=False)
array([[ 0.203125, 0.1875 ]])

Parameters:	lambda1 (float) – Parameter along the reference triangle. lambda2 (float) – Parameter along the reference triangle. lambda3 (float) – Parameter along the reference triangle. _verify (`Optional` [ `bool` ]) – Indicates if the barycentric coordinates should be verified as summing to one and all non-negative (i.e. verified as barycentric). Can either be used to evaluate at points outside the domain, or to save time when the caller already knows the input is verified. Defaults to `True`.
Returns:	The point on the surface (as a two dimensional NumPy array with a single row).
Return type:	numpy.ndarray
Raises:	`ValueError` – If the weights are not valid barycentric coordinates, i.e. they don’t sum to `1`. (Won’t raise if `_verify=False`.) `ValueError` – If some weights are negative. (Won’t raise if `_verify=False`.)

evaluate_cartesian(s, t, _verify=True)¶

Compute a point on the surface.

Evaluates \(B\left(1 - s - t, s, t\right)\) by calling evaluate_barycentric():

>>> nodes = np.array([
...     [0.0 , 0.0  ],
...     [0.5 , 0.5  ],
...     [1.0 , 0.625],
...     [0.0 , 0.5  ],
...     [0.5 , 0.5  ],
...     [0.25, 1.0  ],
... ])
>>> surface = bezier.Surface(nodes, 2)
>>> point = surface.evaluate_cartesian(0.125, 0.375)
>>> point
array([[ 0.16015625, 0.44726562]])
>>> surface.evaluate_barycentric(0.5, 0.125, 0.375)
array([[ 0.16015625, 0.44726562]])

Parameters:	s (float) – Parameter along the reference triangle. t (float) – Parameter along the reference triangle. _verify (`Optional` [ `bool` ]) – Indicates if the coordinates should be verified. See `evaluate_barycentric()`. Defaults to `True`.
Returns:	The point on the surface (as a two dimensional NumPy array).
Return type:	numpy.ndarray

evaluate_multi(param_vals, _verify=True)¶

Compute multiple points on the surface.

If param_vals has two columns, this method treats them as Cartesian: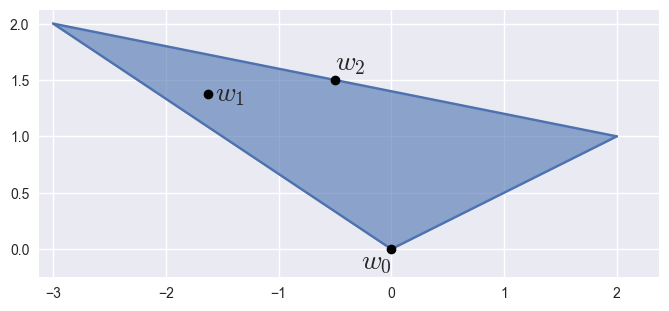

>>> nodes = np.array([
...     [ 0.0, 0.0],
...     [ 2.0, 1.0],
...     [-3.0, 2.0],
... ])
>>> surface = bezier.Surface(nodes, 1)
>>> surface
<Surface (degree=1, dimension=2)>
>>> param_vals = np.array([
...     [0.0  , 0.0  ],
...     [0.125, 0.625],
...     [0.5  , 0.5  ],
... ])
>>> points = surface.evaluate_multi(param_vals)
>>> points
array([[ 0.   , 0.   ],
       [-1.625, 1.375],
       [-0.5  , 1.5  ]])

and if param_vals has three columns, treats them as Barycentric: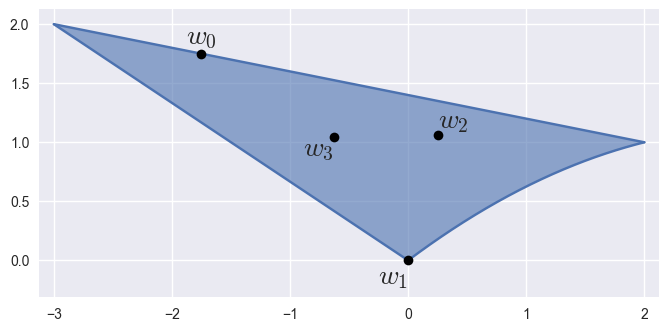

>>> nodes = np.array([
...     [ 0. , 0.  ],
...     [ 1. , 0.75],
...     [ 2. , 1.  ],
...     [-1.5, 1.  ],
...     [-0.5, 1.5 ],
...     [-3. , 2.  ],
... ])
>>> surface = bezier.Surface(nodes, 2)
>>> surface
<Surface (degree=2, dimension=2)>
>>> param_vals = np.array([
...     [0.   , 0.25, 0.75 ],
...     [1.   , 0.  , 0.   ],
...     [0.25 , 0.5 , 0.25 ],
...     [0.375, 0.25, 0.375],
... ])
>>> points = surface.evaluate_multi(param_vals)
>>> points
array([[-1.75  , 1.75    ],
       [ 0.    , 0.      ],
       [ 0.25  , 1.0625  ],
       [-0.625 , 1.046875]])

Note

This currently just uses evaluate_cartesian() and evaluate_barycentric() so is less performant than it could be.

Parameters:	param_vals (numpy.ndarray) – Array of parameter values (as a 2D array). _verify (`Optional` [ `bool` ]) – Indicates if the coordinates should be verified. See `evaluate_barycentric()`. Defaults to `True`.
Returns:	The point on the surface.
Return type:	numpy.ndarray
Raises:	`ValueError` – If `param_vals` is not a 2D array. `ValueError` – If `param_vals` doesn’t have 2 or 3 columns.

plot(pts_per_edge, color=None, ax=None, with_nodes=False, show=False)¶

Plot the current surface.

Parameters:	pts_per_edge (int) – Number of points to plot per edge. color (`Optional` [ `Tuple` [ `float`, `float`, `float` ] ]) – Color as RGB profile. ax (`Optional` [ `matplotlib.artist.Artist` ]) – matplotlib axis object to add plot to. with_nodes (`Optional` [ `bool` ]) – Determines if the control points should be added to the plot. Off by default. show (`Optional` [ `bool` ]) – Flag indicating if the plot should be shown.
Returns:	The axis containing the plot. This may be a newly created axis.
Return type:	matplotlib.artist.Artist
Raises:	`NotImplementedError` – If the surface’s dimension is not `2`.

subdivide()¶

Split the surface into four sub-surfaces.

Does so by taking the unit triangle (i.e. the domain of the surface) and splitting it into four sub-triangles

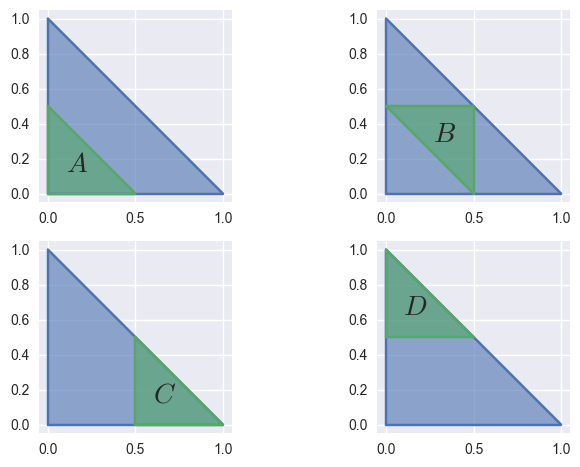
Then the surface is re-parameterized via the map to/from the given sub-triangles and the unit triangle.

For example, when a degree two surface is subdivided:

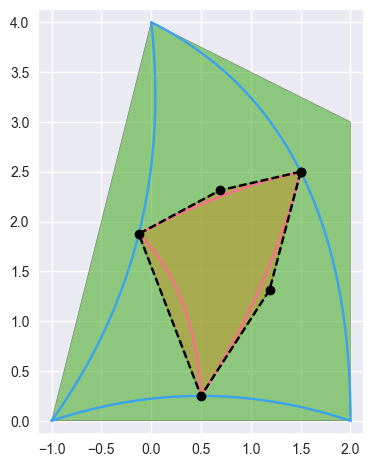
>>> nodes = np.array([
...     [-1.0 , 0.0 ],
...     [ 0.5 , 0.5 ],
...     [ 2.0 , 0.0 ],
...     [ 0.25, 1.75],
...     [ 2.0 , 3.0 ],
...     [ 0.0 , 4.0 ],
... ])
>>> surface = bezier.Surface(nodes, 2)
>>> _, sub_surface_b, _, _ = surface.subdivide()
>>> sub_surface_b
<Surface (degree=2, dimension=2, base=(0.5, 0.5), width=-0.5)>
>>> sub_surface_b.nodes
array([[ 1.5   , 2.5   ],
       [ 0.6875, 2.3125],
       [-0.125 , 1.875 ],
       [ 1.1875, 1.3125],
       [ 0.4375, 1.3125],
       [ 0.5   , 0.25  ]])

Returns:	The lower left, central, lower right and upper left sub-surfaces (in that order).
Return type:	`Tuple` [ `Surface`, `Surface`, `Surface`, `Surface` ]

is_valid¶

bool: Flag indicating if the surface is “valid”.

Here, “valid” means there are no self-intersections or singularities.

This checks if the Jacobian of the map from the reference triangle is nonzero. For example, a linear “surface” with collinear points is invalid:

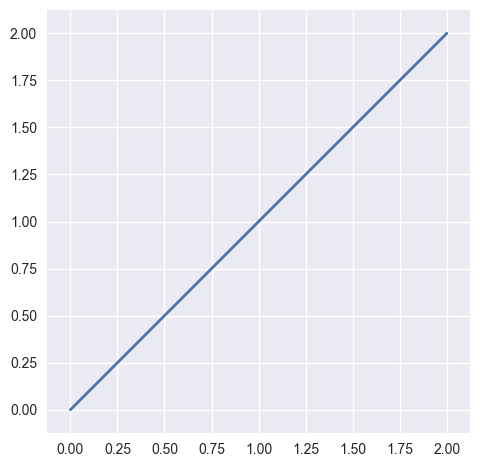
>>> nodes = np.array([
...     [0.0, 0.0],
...     [1.0, 1.0],
...     [2.0, 2.0],
... ])
>>> surface = bezier.Surface(nodes, 1)
>>> surface.is_valid
False

while a quadratic surface with one straight side:

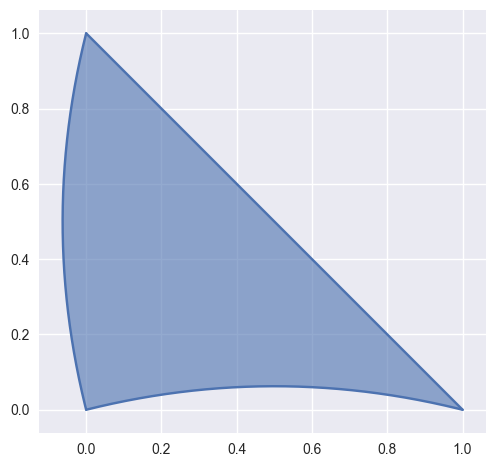
>>> nodes = np.array([
...     [ 0.0  , 0.0  ],
...     [ 0.5  , 0.125],
...     [ 1.0  , 0.0  ],
...     [-0.125, 0.5  ],
...     [ 0.5  , 0.5  ],
...     [ 0.0  , 1.0  ],
... ])
>>> surface = bezier.Surface(nodes, 2)
>>> surface.is_valid
True

though not all higher degree surfaces are valid:

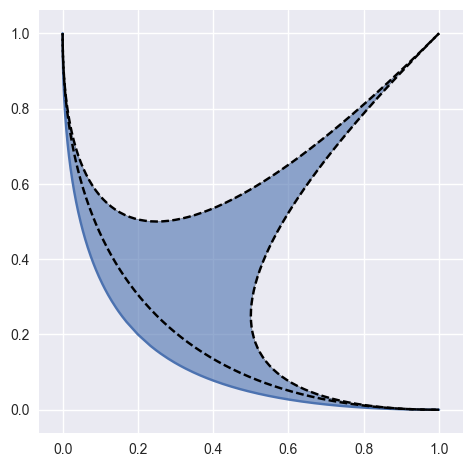
>>> nodes = np.array([
...     [1.0, 0.0],
...     [0.0, 0.0],
...     [1.0, 1.0],
...     [0.0, 0.0],
...     [0.0, 0.0],
...     [0.0, 1.0],
... ])
>>> surface = bezier.Surface(nodes, 2)
>>> surface.is_valid
False

locate(point)¶

Find a point on the current surface.

Solves for \(s\) and \(t\) in \(B(s, t) = p\).

Note

A unique solution is only guaranteed if the current surface is valid. This code assumes a valid surface, but doesn’t check.

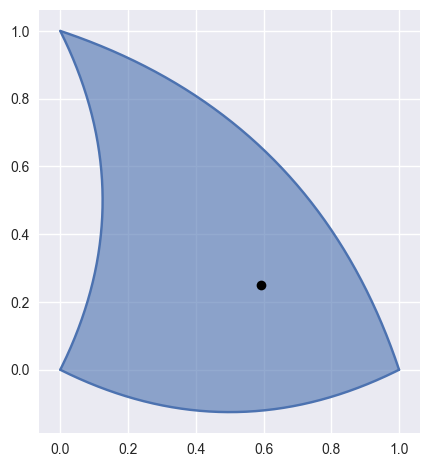
>>> surface = bezier.Surface.from_nodes(np.array([
...     [0.0 ,  0.0 ],
...     [0.5 , -0.25],
...     [1.0 ,  0.0 ],
...     [0.25,  0.5 ],
...     [0.75,  0.75],
...     [0.0 ,  1.0 ],
... ]))
>>> point = np.array([[0.59375, 0.25]])
>>> s, t = surface.locate(point)
>>> s
0.5
>>> t
0.25

Parameters:	point (numpy.ndarray) – A (`1xD`) point on the surface, where \(D\) is the dimension of the surface.
Returns:	The \(s\) and \(t\) values corresponding to `x_val` and `y_val` or `None` if the point is not on the `surface`.
Return type:	`Optional` [ `Tuple` [ `float`, `float` ] ]
Raises:	`NotImplementedError` – If the surface isn’t in \(\mathbf{R}^2\). `ValueError` – If the dimension of the `point` doesn’t match the dimension of the current surface.

intersect(other, _verify=True)¶

Find the common intersection with another surface.

Parameters:	other (Surface) – Other surface to intersect with. _verify (`Optional` [ `bool` ]) – Indicates if extra caution should be used to verify assumptions about the algorithm as it proceeds. Can be disabled to speed up execution time. Defaults to `True`.
Returns:	List of intersections (possibly empty).
Return type:	`List` [ `CurvedPolygon` ]
Raises:	`TypeError` – If `other` is not a surface. `NotImplementedError` – If at least one of the surfaces isn’t two-dimensional.

elevate()¶

Return a degree-elevated version of the current surface.

Does this by converting the current nodes \(\left\{v_{i, j, k}\right\}_{i + j + k = d}\) to new nodes \(\left\{w_{i, j, k}\right\}_{i + j + k = d + 1}\). Does so by re-writing

\[E\left(\lambda_1, \lambda_2, \lambda_3\right) = \left(\lambda_1 + \lambda_2 + \lambda_3\right) B\left(\lambda_1, \lambda_2, \lambda_3\right) = \sum_{i + j + k = d + 1} \binom{d + 1}{i \, j \, k} \lambda_1^i \lambda_2^j \lambda_3^k \cdot w_{i, j, k}\]

In this form, we must have

\[\begin{split}\begin{align*} \binom{d + 1}{i \, j \, k} \cdot w_{i, j, k} &= \binom{d}{i - 1 \, j \, k} \cdot v_{i - 1, j, k} + \binom{d}{i \, j - 1 \, k} \cdot v_{i, j - 1, k} + \binom{d}{i \, j \, k - 1} \cdot v_{i, j, k - 1} \\ \Longleftrightarrow (d + 1) \cdot w_{i, j, k} &= i \cdot v_{i - 1, j, k} + j \cdot v_{i, j - 1, k} + k \cdot v_{i, j, k - 1} \end{align*}\end{split}\]

where we assume that, for example, \(v_{i, j, k - 1}\) is \(0\) (or any other unused value) if \(k = 0\).

>>> surface = bezier.Surface.from_nodes(np.array([
...     [0.0, 0.0],
...     [1.0, 0.0],
...     [0.0, 1.0],
... ]))
>>> surface
<Surface (degree=1, dimension=2)>
>>> new_surface = surface.elevate()
>>> new_surface
<Surface (degree=2, dimension=2)>
>>> new_surface.nodes
array([[ 0. , 0. ],
       [ 0.5, 0. ],
       [ 1. , 0. ],
       [ 0. , 0.5],
       [ 0.5, 0.5],
       [ 0. , 1. ]])

Returns:	The degree-elevated surface.
Return type:	Surface

degree¶: int: The degree of the current shape.

dimension¶

int: The dimension that the shape lives in.

For example, if the shape lives in \(\mathbf{R}^3\), then the dimension is 3.

nodes¶: numpy.ndarray: The nodes that define the current shape.