Curve-Curve Intersection

The problem of intersecting two curves is a difficult one in computational geometry. The Curve.intersect() method uses a combination of curve subdivision, bounding box intersection, and curve approximation (by lines) to find intersections.

Curve-Line Intersection

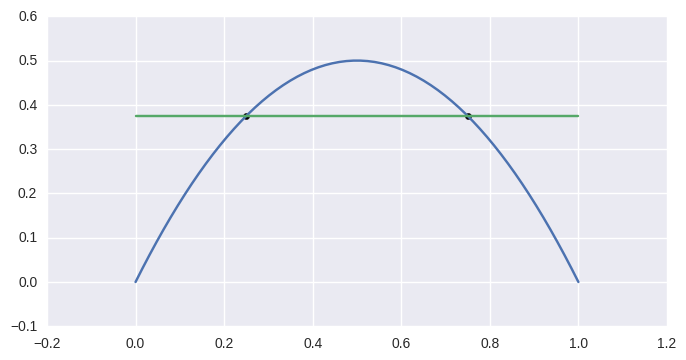
>>> curve1 = bezier.Curve(np.array([
...     [0.0, 0.0],
...     [0.5, 1.0],
...     [1.0, 0.0],
... ]))
>>> curve2 = bezier.Curve(np.array([
...     [0.0, 0.375],
...     [1.0, 0.375],
... ]))
>>> curve1.intersect(curve2)
array([[ 0.25 , 0.375],
       [ 0.75 , 0.375]])
_images/test_curves1_and_8.png 
>>> curve1 = bezier.Curve(np.array([
...     [0.0, 0.0],
...     [0.5, 1.0],
...     [1.0, 0.0],
... ]))
>>> curve2 = bezier.Curve(np.array([
...     [0.5, 0.0 ],
...     [0.5, 0.75],
... ]))
>>> curve1.intersect(curve2)
array([[ 0.5, 0.5]])
_images/test_curves1_and_9.png 
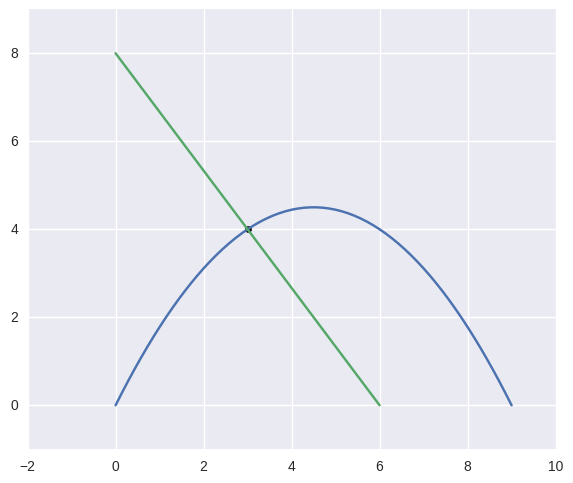
>>> curve1 = bezier.Curve(np.array([
...     [0.0, 0.0],
...     [4.5, 9.0],
...     [9.0, 0.0],
... ]))
>>> curve2 = bezier.Curve(np.array([
...     [0.0, 8.0],
...     [6.0, 0.0],
... ]))
>>> curve1.intersect(curve2)
array([[ 3., 4.]])
_images/test_curves10_and_11.png 
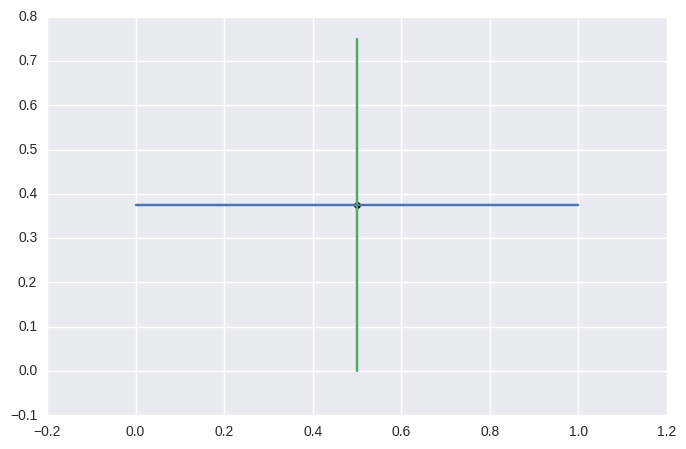
>>> curve1 = bezier.Curve(np.array([
...     [0.0, 0.375],
...     [1.0, 0.375],
... ]))
>>> curve2 = bezier.Curve(np.array([
...     [0.5, 0.0 ],
...     [0.5, 0.75],
... ]))
>>> curve1.intersect(curve2)
array([[ 0.5 , 0.375]])
_images/test_curves8_and_9.png

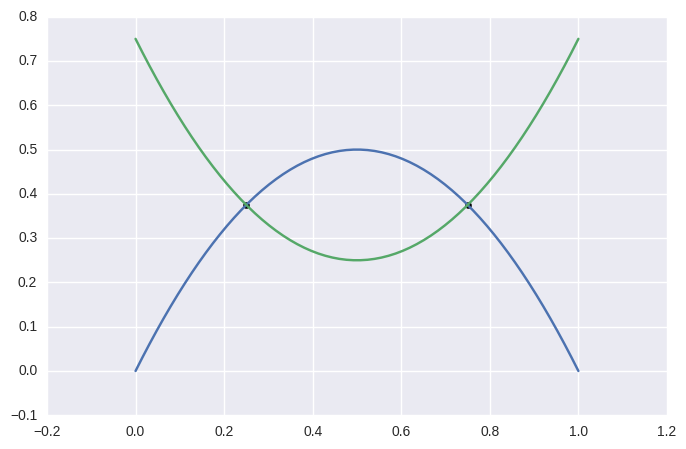
Curved Intersections

For curves which intersect at exact floating point numbers, we can typically compute the intersection with zero error:

>>> curve1 = bezier.Curve(np.array([
...     [0.0, 0.0],
...     [0.5, 1.0],
...     [1.0, 0.0],
... ]))
>>> curve2 = bezier.Curve(np.array([
...     [0.0,  0.75],
...     [0.5, -0.25],
...     [1.0,  0.75],
... ]))
>>> curve1.intersect(curve2)
array([[ 0.25 , 0.375],
       [ 0.75 , 0.375]])
_images/test_curves1_and_5.png 
>>> curve1 = bezier.Curve(np.array([
...     [0.0, 0.0],
...     [1.5, 3.0],
...     [3.0, 0.0],
... ]))
>>> curve2 = bezier.Curve(np.array([
...     [ 3.0  ,  1.5    ],
...     [ 2.625, -0.90625],
...     [-0.75 ,  2.4375 ],
... ]))
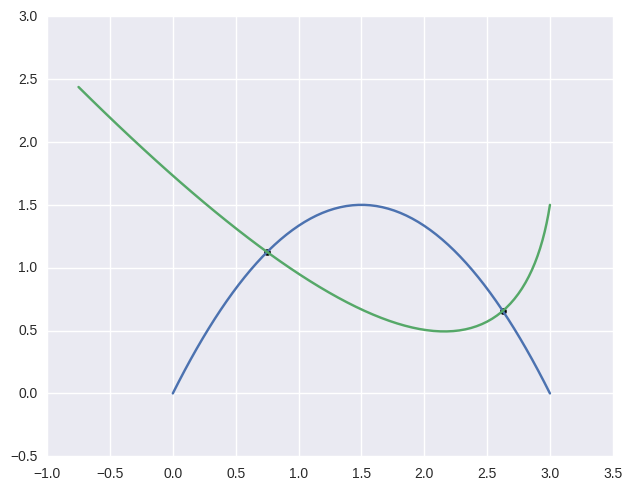
>>> curve1.intersect(curve2)
array([[ 0.75  , 1.125  ],
       [ 2.625 , 0.65625]])
_images/test_curves3_and_4.png 
>>> curve1 = bezier.Curve(np.array([
...     [0.0  , 0.0  ],
...     [0.375, 0.75 ],
...     [0.75 , 0.375],
... ]))
>>> curve2 = bezier.Curve(np.array([
...     [0.25 , 0.5625],
...     [0.625, 0.1875],
...     [1.0  , 0.9375],
... ]))
>>> curve1.intersect(curve2)
array([[ 0.375 , 0.46875],
       [ 0.625 , 0.46875]])
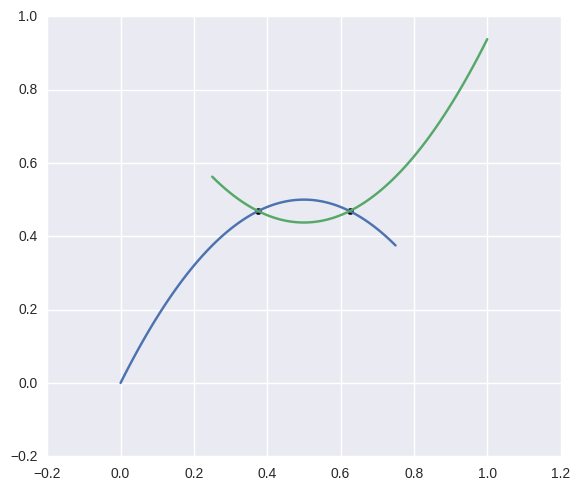
_images/test_curves14_and_16.png

Even for curves which don’t intersect at exact floating point numbers, we can compute the intersection to machine precision:

>>> curve1 = bezier.Curve(np.array([
...     [0.0, 0.0],
...     [0.5, 1.0],
...     [1.0, 0.0],
... ]))
>>> curve2 = bezier.Curve(np.array([
...     [1.125,  0.5],
...     [0.625, -0.5],
...     [0.125,  0.5],
... ]))
>>> intersections = curve1.intersect(curve2)
>>> sq31 = np.sqrt(31.0)
>>> expected = np.array([
...     [36 - 4 * sq31, 16 + sq31],
...     [36 + 4 * sq31, 16 - sq31],
... ]) / 64.0
>>> max_err = np.max(np.abs(intersections - expected))
>>> np.log2(max_err)
-54.0
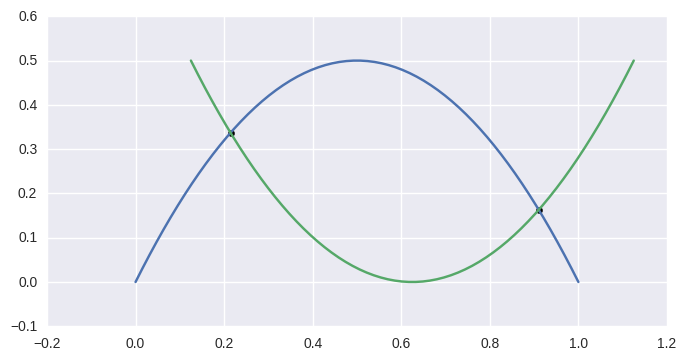
_images/test_curves1_and_2.png 
>>> curve1 = bezier.Curve(np.array([
...     [0.0, 0.0],
...     [0.5, 1.0],
...     [1.0, 0.0],
... ]))
>>> curve2 = bezier.Curve(np.array([
...     [0.0, 0.265625],
...     [0.5, 0.234375],
...     [1.0, 0.265625],
... ]))
>>> intersections = curve1.intersect(curve2)
>>> sq33 = np.sqrt(33.0)
>>> expected = np.array([
...     [33 - 4 * sq33, 17],
...     [33 + 4 * sq33, 17],
... ]) / 66.0
>>> max_err = np.max(np.abs(intersections - expected))
>>> np.log2(max_err)
-54.0
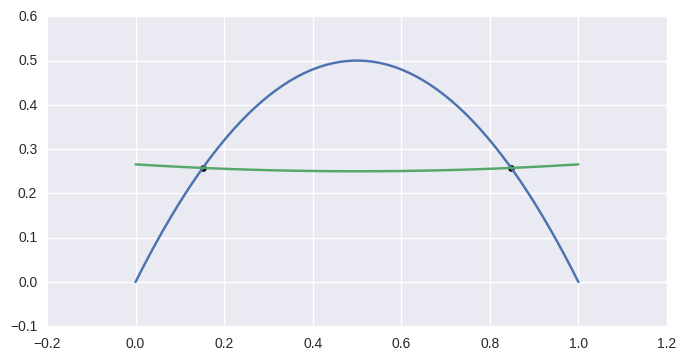
_images/test_curves1_and_7.png 
>>> curve1 = bezier.Curve(np.array([
...     [0.0, 0.0],
...     [0.5, 1.0],
...     [1.0, 0.0],
... ]))
>>> curve2 = bezier.Curve(np.array([
...     [0.0 ,  0.0],
...     [0.25,  2.0],
...     [0.5 , -2.0],
...     [0.75,  2.0],
...     [1.0 ,  0.0],
... ]))
>>> intersections = curve1.intersect(curve2)
>>> sq7 = np.sqrt(7.0)
>>> expected = np.array([
...     [7 - sq7, 6],
...     [7 + sq7, 6],
...     [      0, 0],
...     [     14, 0],
... ]) / 14.0
>>> max_err = np.max(np.abs(intersections - expected))
>>> np.log2(max_err)
-54.0
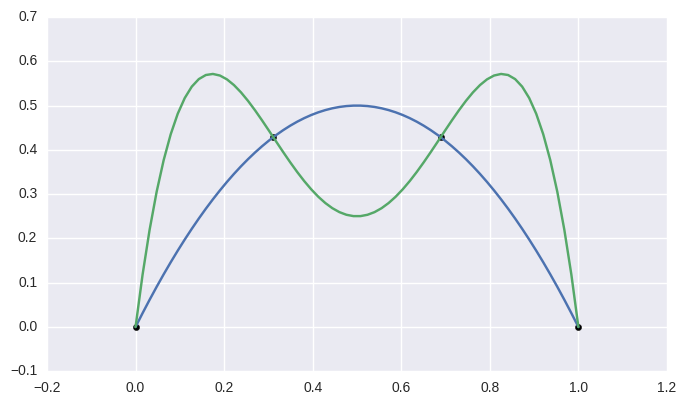
_images/test_curves1_and_13.png 
>>> curve1 = bezier.Curve(np.array([
...     [-0.125, -0.28125],
...     [ 0.5  ,  1.28125],
...     [ 1.125, -0.28125],
... ]))
>>> curve2 = bezier.Curve(np.array([
...     [ 1.5625, -0.0625],
...     [-1.5625,  0.25  ],
...     [ 1.5625,  0.5625],
... ]))
>>> intersections = curve1.intersect(curve2)
>>> sq5 = np.sqrt(5.0)
>>> expected = np.array([
...     [6 - 2 * sq5, 5 - sq5],
...     [          4, 6      ],
...     [         16, 0      ],
...     [6 + 2 * sq5, 5 + sq5],
... ]) / 16.0
>>> max_err = np.max(np.abs(intersections - expected))
>>> np.log2(max_err)
-50.415...
_images/test_curves21_and_22.png

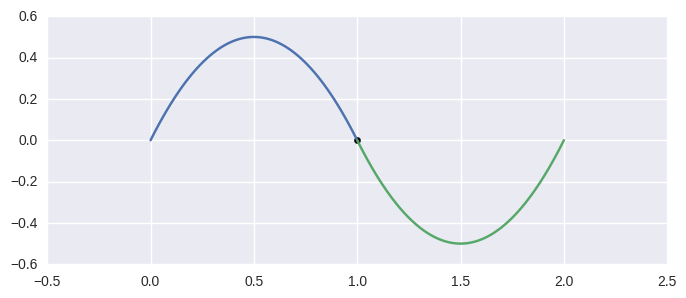
Intersections at Endpoints

>>> curve1 = bezier.Curve(np.array([
...     [0.0, 0.0],
...     [0.5, 1.0],
...     [1.0, 0.0],
... ]))
>>> curve2 = bezier.Curve(np.array([
...     [1.0,  0.0],
...     [1.5, -1.0],
...     [2.0,  0.0],
... ]))
>>> curve1.intersect(curve2)
array([[ 1., 0.]])
_images/test_curves1_and_18.png 
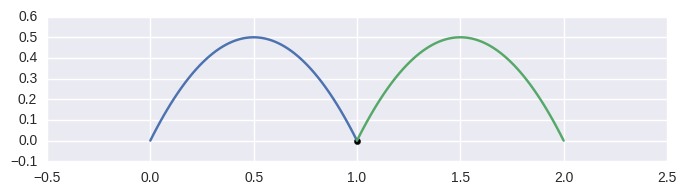
>>> curve1 = bezier.Curve(np.array([
...     [0.0, 0.0],
...     [0.5, 1.0],
...     [1.0, 0.0],
... ]))
>>> curve2 = bezier.Curve(np.array([
...     [2.0, 0.0],
...     [1.5, 1.0],
...     [1.0, 0.0],
... ]))
>>> curve1.intersect(curve2)
array([[ 1., 0.]])
_images/test_curves1_and_19.png 
>>> curve1 = bezier.Curve(np.array([
...     [0.0, 0.0],
...     [4.5, 9.0],
...     [9.0, 0.0],
... ]))
>>> curve2 = bezier.Curve(np.array([
...     [11.0,  8.0],
...     [ 7.0, 10.0],
...     [ 3.0,  4.0],
... ]))
>>> curve1.intersect(curve2)
array([[ 3., 4.]])
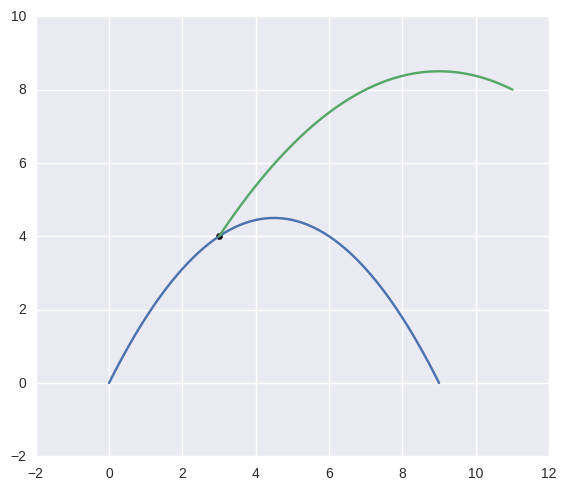
_images/test_curves10_and_17.png

Detecting Self-Intersections

>>> curve1 = bezier.Curve(np.array([
...     [ 0.0 , 0.0  ],
...     [-1.0 , 0.0  ],
...     [ 1.0 , 1.0  ],
...     [-0.75, 1.625],
... ]))
>>> left, right = curve1.subdivide()
>>> left.intersect(right)
array([[-0.09375 , 0.578125]])
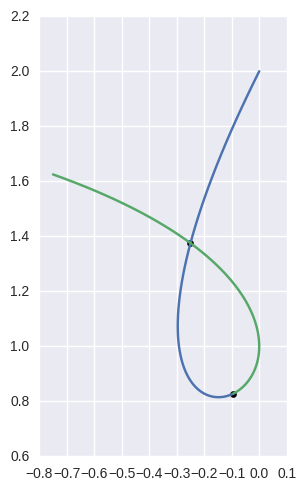
_images/test_curve12_self_crossing.png

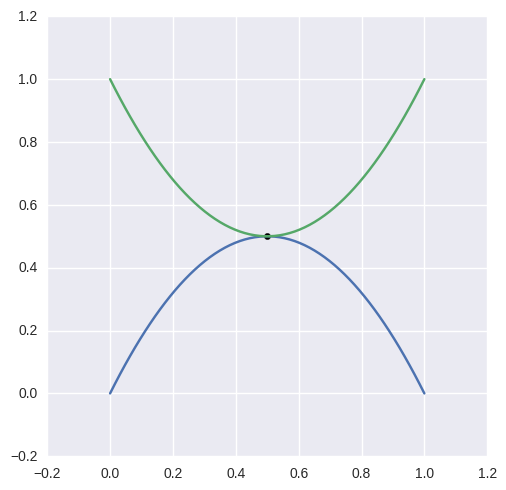
Limitations

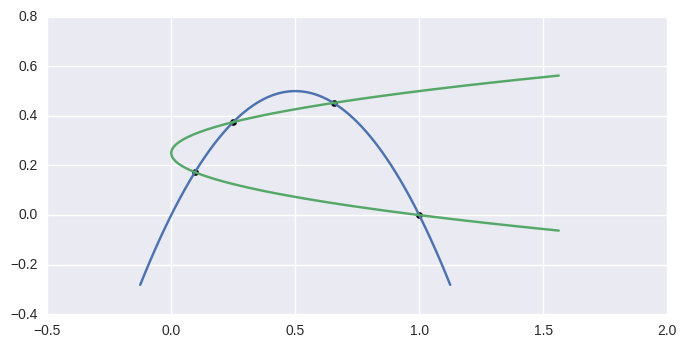
Intersections that occur at points of tangency are in general problematic. For example, consider

\[\begin{split}B_1(s) = \left[ \begin{array}{c} s \\ 2s(1 - s)\end{array}\right], \quad B_2(t) = \left[ \begin{array}{c} t \\ t^2 + (1 - t)^2 \end{array}\right]\end{split}\]

The first curve is the zero set of \(y - 2x(1 - x)\), so plugging in the second curve gives

\[0 = t^2 + (1 - t)^2 - 2t(1 - t) = (2t - 1)^2.\]

This shows that a point of tangency is equivalent to a repeated root of a polynomial. For this example, the intersection process successfully terminates

>>> curve1 = bezier.Curve(np.array([
...     [0.0, 0.0],
...     [0.5, 1.0],
...     [1.0, 0.0],
... ]))
>>> curve2 = bezier.Curve(np.array([
...     [0.0, 1.0],
...     [0.5, 0.0],
...     [1.0, 1.0],
... ]))
>>> curve1.intersect(curve2)
array([[ 0.5, 0.5]])
_images/test_curves1_and_6.png

However this library mostly avoids (for now) computing tangent intersections. For example, the curves

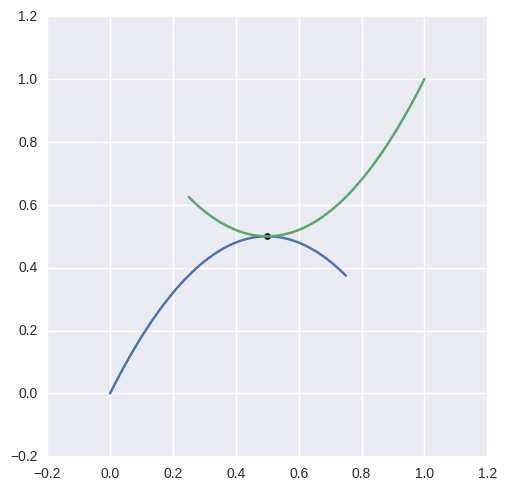
_images/test_curves14_and_15.png

have a tangent intersection that this library fails to compute:

>>> curve1 = bezier.Curve(np.array([
...     [0.0  , 0.0  ],
...     [0.375, 0.75 ],
...     [0.75 , 0.375],
... ]))
>>> curve2 = bezier.Curve(np.array([
...     [0.25 , 0.625],
...     [0.625, 0.25 ],
...     [1.0  , 1.0  ],
... ]))
>>> curve1.intersect(curve2)
Traceback (most recent call last):
  ...
NotImplementedError: Delta_0 x Delta_1 = 0 not supported

This failure comes from the fact that the linear approximations of the curves near the point of intersection are parallel.

As above, we can find some cases where tangent intersections are resolved:

>>> curve1 = bezier.Curve(np.array([
...     [0.0, 0.0],
...     [4.5, 9.0],
...     [9.0, 0.0],
... ]))
>>> curve2 = bezier.Curve(np.array([
...     [3.0, 4.5],
...     [8.0, 4.5],
... ]))
>>> curve1.intersect(curve2)
array([[ 4.5, 4.5]])
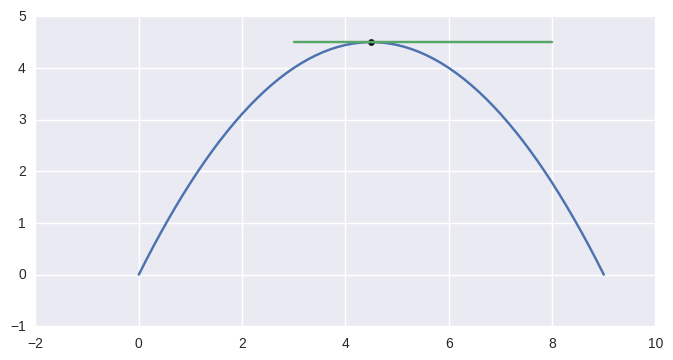
_images/test_curves10_and_23.png

In addition to points of tangency, coincident curve segments are (for now) not supported. For the curves

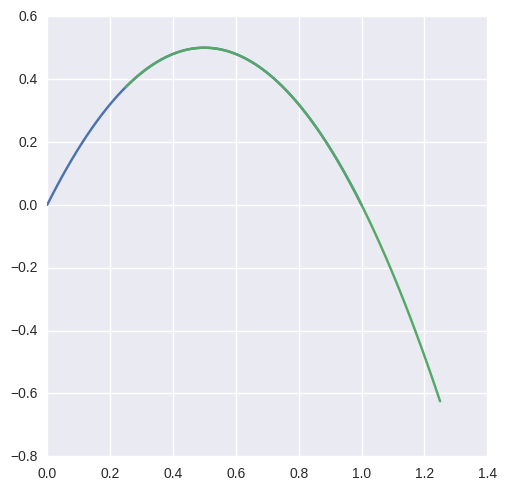
_images/test_curves1_and_24.png

the library fails as well

>>> curve1 = bezier.Curve(np.array([
...     [0.0, 0.0],
...     [0.5, 1.0],
...     [1.0, 0.0],
... ]))
>>> curve2 = bezier.Curve(np.array([
...     [0.25,  0.375],
...     [0.75,  0.875],
...     [1.25, -0.625],
... ]))
>>> curve1.intersect(curve2)
Traceback (most recent call last):
  ...
NotImplementedError: The number of candidate intersections is too high.