bezier
Helper for Bézier Curves, Triangles, and Higher Order Objects
This library provides:
Dive in and take a look!
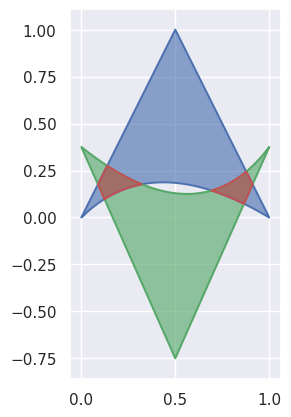
Why Bézier?
A Bézier curve (and triangle, etc.) is a parametric curve that uses the Bernstein basis:
to define a curve as a linear combination:
This comes from the fact that the weights sum to one:
This can be generalized to higher order by considering three, four, etc. non-negative weights that sum to one (in the above we have the two non-negative weights \(s\) and \(1 - s\)).
Due to their simple form, Bézier curves:
- can easily model geometric objects as parametric curves, triangles, etc.
- can be computed in an efficient and numerically stable way via de Casteljau’s algorithm
- can utilize convex optimization techniques for many algorithms (such as curve-curve intersection), since curves (and triangles, etc.) are convex combinations of the basis
Many applications – as well as the history of their development – are described in “The Bernstein polynomial basis: A centennial retrospective”, for example;
Installing
The bezier Python package can be installed with pip:
$ python -m pip install --upgrade bezier
$ python3.11 -m pip install --upgrade bezier
$ # To install optional dependencies, e.g. SymPy
$ python -m pip install --upgrade bezier[full]
To install a pure Python version (i.e. with no binary extension):
$ BEZIER_NO_EXTENSION=true \
> python -m pip install --upgrade bezier --no-binary=bezier
bezier is open-source, so you can alternatively grab the source
code from GitHub and install from source.
Getting Started
For example, to create a curve:
>>> import bezier
>>> import numpy as np
>>> nodes1 = np.asfortranarray([
... [0.0, 0.5, 1.0],
... [0.0, 1.0, 0.0],
... ])
>>> curve1 = bezier.Curve(nodes1, degree=2)
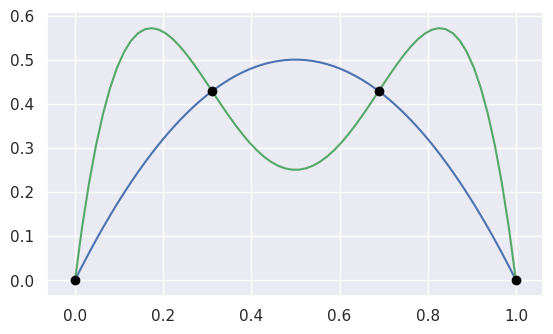
The intersection (points) between two curves can also be determined:
>>> nodes2 = np.asfortranarray([
... [0.0, 0.25, 0.5, 0.75, 1.0],
... [0.0, 2.0 , -2.0, 2.0 , 0.0],
... ])
>>> curve2 = bezier.Curve.from_nodes(nodes2)
>>> intersections = curve1.intersect(curve2)
>>> intersections
array([[0.31101776, 0.68898224, 0. , 1. ],
[0.31101776, 0.68898224, 0. , 1. ]])
>>> s_vals = np.asfortranarray(intersections[0, :])
>>> points = curve1.evaluate_multi(s_vals)
>>> points
array([[0.31101776, 0.68898224, 0. , 1. ],
[0.42857143, 0.42857143, 0. , 0. ]])
and then we can plot these curves (along with their intersections):
>>> import seaborn
>>> seaborn.set()
>>>
>>> ax = curve1.plot(num_pts=256)
>>> _ = curve2.plot(num_pts=256, ax=ax)
>>> lines = ax.plot(
... points[0, :], points[1, :],
... marker="o", linestyle="None", color="black")
>>> _ = ax.axis("scaled")
>>> _ = ax.set_xlim(-0.125, 1.125)
>>> _ = ax.set_ylim(-0.0625, 0.625)
For API-level documentation, check out the Bézier Python package documentation.
Development
To work on adding a feature or to run the functional tests, see the DEVELOPMENT doc for more information on how to get started.
Citation
For publications that use bezier, there is a JOSS paper that can be
cited. The following BibTeX entry can be used:
@article{Hermes2017,
doi = {10.21105/joss.00267},
url = {https://doi.org/10.21105%2Fjoss.00267},
year = {2017},
month = {Aug},
publisher = {The Open Journal},
volume = {2},
number = {16},
pages = {267},
author = {Danny Hermes},
title = {Helper for B{\'{e}}zier Curves, Triangles, and Higher Order Objects},
journal = {The Journal of Open Source Software}
}
A particular version of this library can be cited via a Zenodo DOI; see a full list by version.
License
bezier is made available under the Apache 2.0 License. For more
details, see the LICENSE.
